oohcode

$\bigodot\bigodot^H \rightarrow CODE$

csapp chapter6:存储器层次结构

存储器系统(memory system)是一个具有不同容量、成本和访问时间的存储设备的层次结构。程序如何利用存储器的特性提高性能呢？这将是本章主要探讨的内容。

存储技术

计算机的的成功很大程度上源自于存储技术的巨大进步。下面这幅图是存储器的层次结构：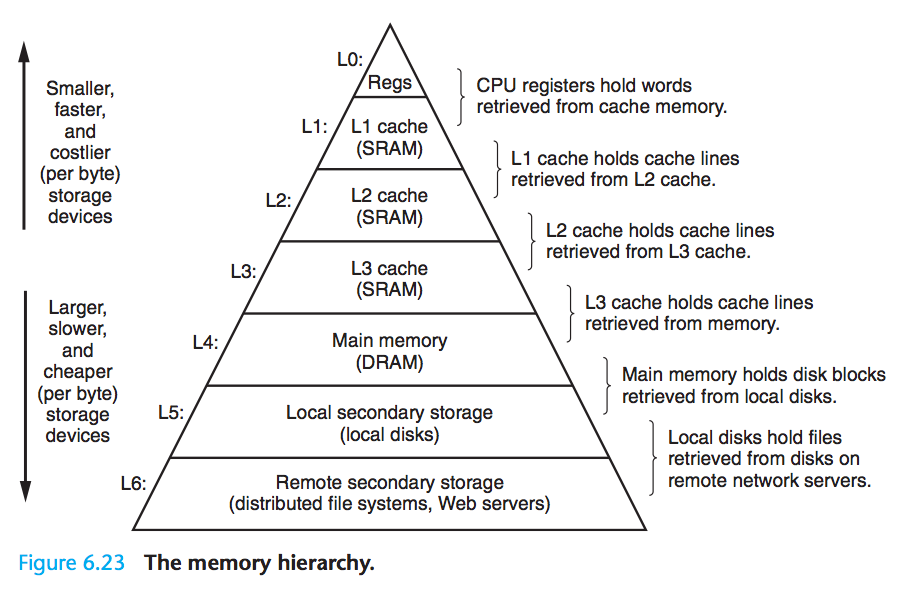

从上到下，存储的速度越慢，容量越大。
关于存储器内部是实现方式这就不介绍了，重点介绍一下计算机存储器的运行方式。
存储器层次结构的中心思想，对于每个k层，位于k层的更快更小的存储设备作为位于k+1层的跟大更慢的存储设备的缓存。也就是说层次结构中的k层的数据都是来自k+1层的。数据在每层之间的传送是以块大小为传送单元的。不同层之间的块大小可以不一样。程序运行过程中，对存储器的运用分为两种情况：

  • 缓存命中: 当程序需要数据时，最先从最高的层开始查找，如果没有找到了所需的数据，就是缓存命中。
  • 缓存不命中: 当所需的数据从当前层没有找到，就叫缓存不命中。这时候就会从下一层开始查找，直到找到所需的数据为止。当找到所需的数据后，数据会再次经过上面的层，把找到的数据保存到上面的层中，这时就要覆盖上面层的数据，如何覆盖，这涉及到替换策略，不再详述。

通过上面存储器的使用方式，可以看出，要想提高程序的性能，就必须利用时间局部性和空间局部性。

  • 时间局部性: 如果一个数据被加载到了最上层，那么如果连续多次调用这个数据就不需要去其他层寻找，减少了数据寻找和写缓存的过程，大大提高到了利用效率。
  • 空间局部性： 但一个数被加载的最上层时，由于数据时以块大小进行传递的，所以这个数据相邻的地址数据也会被传递，所以如果这时候访问相邻的数据话，很有可能就在这一层，而不需要去其他层寻找数据，也大大提高了利用率。

下面通过一个程序来说明一下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int sum1(int a[M][N])
{
    int i, j, sum = 0;

    for(i = 0; i < M; i++)
        for(j = 0; j < N; j++)
            sum += a[i][j];
    return sum;
}

int sum2(int a[M][N])
{
    int i, j, sum = 0;

    for(j = 0; j < M; j++)
        for(i = 0; i < N; i++)
            sum += a[i][j];
    return sum;
}

对于sum1和sum2两个程序都时求一个二纬数组的和，唯一不同的是循环变量，也就是数组的下标顺序不一样。对于sum1，由于二纬数组是顺序存储的，而求和的时候也是按照递增的地址顺序求和的，这很好的利用了空间局部性这个原理，而sum2，同样是求和，但是二维数组的顺序并不是顺序访问的，又跳跃，所以每次访问的地址不是连续的，没有很好的利用空间局部性的原理，效率要低很多。
另一方面，两个程序的循环的过程中都使用了一个auto变量sum，每次循环都访问这个变量的值，这很好的利用了时间局部性原理。

CSAPP