垃圾回收基本算法

本章介绍GC的基本算法:GC标记-清除法，引用计数法, GC复制算法。这三种我认为是GC的三个方向的基本思维。其他方法都是围绕这个些基本方法展开的。

GC标记-清除法

基本方法

所谓的标记-清除法，依据其字面意思就是，先做标记，然后在清除。这个过程分为两个阶段，标记阶段就是把所有活动对象坐上标记，清除阶段就是把那些没有做标记的对象，也就是非活动对象回收的阶段。利用伪代码表示就是:

mark_sweep() {
    mark_phase()
    sweep_phase()
}

• 标记阶段: 这个阶段从根出发，利用深度优先遍历(不用广度优先是因为深度优先搜索比广度优先搜索更能压低内存使用量。), 对每个能到达的活动对象都做上标记(用一个位来表示)。这个阶段所花费的时间与”活动对象的总数”成正比。标记阶段伪代码:

  mark_phase() {
      #遍历根节点, 进行标记
      for(r: $roots)
          mark(*r)
  }
  #标记函数
  mark(obj) {
      if(obj.mark == FALSE)
          obj.mark = TRUE
          #深度优先遍历
          for(child : children(obj))
              mark(*child)
  }

• 清除阶段: 清除阶段主要工作是通过遍历整个堆，把未被标记的对象(非活动对象)回收再利用。回收对象就是把对象作为分块，连接到被称为”空闲链表”的单向链表。之后进行分配时遍历空闲链表就可以找到分块了。两个相邻的分块如果地址是连续的，就会对其进行合并, 合并操作可以减少碎片的发生。清除阶段的伪代码:

  sweep_phase() {
      sweeping = $heap_start
      #遍历堆
      while(sweeping < $head_end)
          if(sweeping.mark == TRUE)
              sweeping.mark == FALSE
          else
              #放入空闲链表
              if(sweeping.mark == $free_list + $free_list.size)
                  #合并
                  $free_list.size += sweeping.size
              else
                  sweeping.next = $free_list
                  $free_list = sweeping
              sweeping += sweeping.size
  }

• 分配: 进行mutator申请分块时，搜索空闲链表并找到合适大小的分块，这个过程就叫做分配。找到合适的分块大小有三种策略:

  1. First-fit: 找到最初发现大于等于size的分块就立刻返回。考虑到分配所需的时间，标记清除法选择的就是这种方法。
  2. Best-fit: 遍历空闲链表，找到大于等于size的最小分块返回。
  3. Worst-fit: 找出最大的分块，把分块分割成size大小和剩余分块。
     分配阶段的伪代码:

     new_obj(size) {
         chunk = pickup_chunk(size, $free_list)
         if(chunk != NULL)
             return chunk
         else
             allocation_fail()
     }

优点/缺点

• 优点:
  1. 实现简单
  2. 与保守式GC算法兼容: 保守式算法就是不知道对象是否是指针，所以移动对象会造成错误(后面会讲到), 而标记清除算法是不会移动对象的，所以是兼容的。
• 缺点:
  1. 碎片化: 由于非活动对象分布不均匀，容易照成堆内的内存空间碎片化，不利于mutator的执行。
  2. 分配速度: 由于分配时需要遍历空闲链表，查找速度取决于要分配的块和空闲链表的分布。后面要讲到的复制算法和标记-压缩算法由于分块是连续内存分布的，所以速度要快。
  3. 与写时复制技术不兼容： 因为每次GC都要修改活动对象的标记位，导致写操作的发生，从而产生复制。

多个空闲链表

为了提高分配速度，一个改进就是把分块按照大小分为多个空闲链表，这样在分配的时候就可以根据要分配的空间的大小去对应的空闲链表中寻找，大大减少了查找分块的时间。
下面是利用多个空闲链表的new_obj()函数

new_obj(size){
    #index 是一个要分配的字的大小
    index = size / (WORD_LENGTH / BYTE_LENGTH)
    #空闲链表一共有101个，0-100都是按照字精确分配到对应的$free_list[index]中，
    #大于100的字都分配到$free_list[101]中
    if(index <= 100)
        if($free_list[index] != NULL)
            #直接找到对应的空闲链表
            chunk = $free_list[index]
            $free_list[index] = $free_list[index].next
            return chunk
    else 
        #大于100的需要遍历$free_list[101]找到合适大小的块
        chunk = pickup_chunk(size, $free_list[101])
        if(chunk != NULL)
            return chunk

    allocation_fail()
}

BiBOP法

针对标记-清除算法的碎片化问题, 可以把堆先分割成大小固定的块，让每个块只能配置同样大小的对象，这就是BiBOP法。如果某个大小字的活动对象很少，其他的字活动对象很多的话，这种情况也不能提高堆的利用率，无法解决碎片化的问题。

位图标记法

上面还说道标记-清除法不能够与写时复制技术兼容是因为修改标记位会引起复制发生，为了解决这个问题，位图标记法采用只收集各个对象的标志位并表格化，不跟对象一起管理。也就是把对象和标记位进行了分离。这样做有两个好处:

1. 与写时复制技术兼容: 因为GC的时候改变了标记位也不会引起对象的复制, 而位图表格非常小，所以即使被复制也不会有什么大的影响。
2. 清除操作更高效: 在遍历堆的时候不需要取消标志位，可以最后在位图表格中设置。

延迟清除法

延迟清除法(Lazy Sweep)是缩减因清除操作而导致的mutator最大暂停时间的方法。这个方法的伪代码如下:

new_obj(size){
    #用延迟清除法找到对应的块
    chunk = lazy_sweep(size)
    if(chunk != NULL)
        return chunk
    #没有找到合适的，进行一次标记操作
    mark_phase()
    #再用延迟清除法找到对应的块 
    chunk = lazy_sweep(size)
    if(chunk != NULL)
        return chunk
     
    allocation_fail()
}

lazy_sweep(size){
    while($sweeping < $head_end)
        if($sweeping.mark == TRUE)
            $sweeping.mark == FALSE
        #找到和大小合适的块
        else if($sweeping.size > size)
            chunk = $sweeping
            $sweeping += $sweeping + $sweeping.size
            return chunk
        #没找到继续往下找
        $sweeping += $sweeping + $sweeping.size
    #遍历完了也没找到，$sweeping置为从头开始
    $sweeping = $heap_start
    return NULL
}

这里跟之前不同的是$sweeping是一个全局变量，每次执行lazy_sweep的时候都会从当前$sweeping的位置往后查找。如果第一次没有找到，第二次就会从头开始查找，如果第二次也没有查到，那就是没有可以分配的块了。一般情况下第一次查找范围变小了，mutator的执行时间就短了。但是有一个问题是就是当数据分配不均，比如说后面的都是活动对象，前面的都是空的，反而会增加mutator的时间。如何改善这个问题，后面会再说到。

引用计数法

GC的目的是为了释放无法被引用的对象，自然就会想到让每个对象记录下自己被引用的个数，如果个数为0表示无法被引用，那就可以对其进行回收。这种思路就是引用计数法(Reference Counting)。

基本方法

引用计数法最重要的就是引入了一个计数器，用来记录被引用的个数。首先先看一下引用计数法的伪代码实现:

#生成新对象
new_obj(size){
    #从空闲链表中找到合适的块
    obj = pickup_chunk(size, $free_list)

    if(obj == NULL)
        allocation_fail()
    else
        #对象有一个计数器，成功生成后计数器值是1
        obj.ref_cnt = 1
        return obj
}

#更新ptr指针，使其指向新对象obj
update_ptr(ptr, obj){
    #被指向的对象计数器+1
    inc_ref_cnt(obj)
    #原来指向的对象计数器-1
    dec_ref_cnt(*ptr)
    #指向新对象
    *ptr = obj
}

#计数器+1
inc_ref_cnt(obj){
    obj.ref_cnt++
}

#计数器-1
dec_ref_cnt(obj){
    #obj计数器-1
    obj.ref_cnt--
    #obj计数器为0，说明对象变成了"垃圾", 需要对其子对象计数器都-1， 因为这个对象不存在了。
    if(obj.ref_cnt == 0)
        for(child : children(obj))
            dec_ref_cnt(*child)
        #将obj连接到空闲链表中
        reclaim(obj)
}

上面需要注意的一点是执行update_ptr的时候先执行了inc_ref_cnt后执行了dec_ref_cnt, 这是因为当update_ptr的前后两个对象是同一个时，如果先指向了dec_ref_cnt就会把这个对象删除，再执行inc_ref_cnt时就会出错，而顺序反过来就不会存在这个问题了。还有一点是引用计数法和标记清除法不一样的地方:引用计数法会在指针变动时发现是否是垃圾，从而立即回收，而标记清除法则即使发现了也不会立即回收，而是标记完后一起回收。

优点/缺点

• 优点

  1. 可以即刻进行垃圾回收
  2. 最大暂停时间短: 只在发生引用关系变化时立即回收。
  3. 没有必要沿指针查找: 根据每个变量的引用计数来回收，不需要进行遍历。

• 缺点

  1. 计数器值的增减处理繁重
  2. 计数器需要占用很多位: 计数器需要记录被引用的个数，这个记录位会占用不少的内存空间。
  3. 实现繁琐复杂
  4. 循环引用无法回收:

     class Person {
         string name
         Person lover
     }
     
     taro = new Person("太郎") //执行后taro的引用计数为1
     hanako = new Person("花子") //执行后hanako的引用计数为1
     taro.lover = hanako //执行后hanako的引用计数为2
     hanako.lover = taro //执行后taro的引用计数为2
     taro = null //taro指向null, hanako引用计数-1，变为1
     hanako = null //hanako指向null, taro引用计数-1， 变为1
     //全部执行完后taro与hanako的引用计数都为1，不能被回收，但是又无法被引用, 照成了内存泄露的情况

用图来说请其中的过程如下：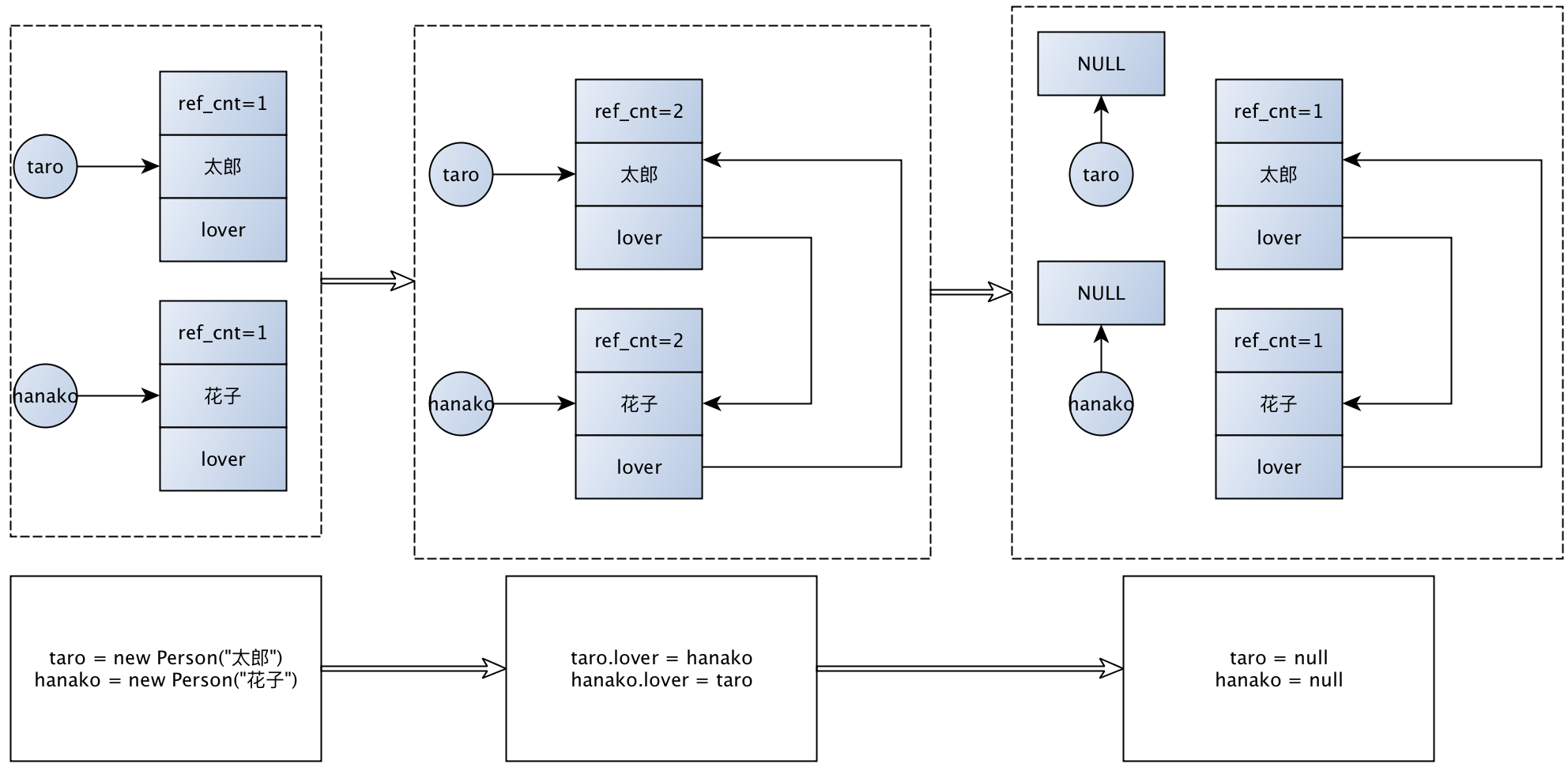

延迟引用计数法

上面说到引用计数法的计数器值得增减处理很繁重，为了改善这个缺点，引入了延迟引用计数法(Deferred Reference Counting)。延迟引用计数法利用ZCT(Zero Count Table)来记录计时器值在dec_ref_cnt()作用下变为0的对象, zct表内的值是指向这些对象的指针。

#update_ptr($ptr, obj)调用不变，只是dec_ref_cnt不会递每次都递归处理子节点的引用计数
dec_ref_cnt(obj){
    obj.ref_cnt--
    if(obj.ref_cnt == 0)
        #$zct满了就执行一次扫描
        if(is_full($zct) == TRUE)
            scan_zct()
        push($zct, obj)
}

new_obj(size){
    obj = pickup_chunk(size, $free_list)

    if(obj == NULL)
        #空间不够执行一次扫描, 释放空间
        scan_zct()
        obj = pickup_chunk(size, $free_list)
        if(obj == NULL)
            allocation_fail()

    obj.ref_cnt = 1
    return obj
}
#扫描zct
scan_zct(){
    #对根直接引用的对象都进行增量， 把根引用反映到计数器的值上
    for(r : $roots)
        (*r).ref_cnt++
    #对子对象的计数器进行减量操作，回收 
    for(obj : $zct)
        if(obj.ref_cnt == 0)
            remove($zct, obj)
            delete(obj)
    #恢复根节点直接引用的对象计数器的值
    for(r : $roots)
        (*r).ref_cnt--
}

#减量操作和回收
delete(obj){
    for(child : children(obj))
        (*child).ref_cnt--
        if((*child).ref_cnt == 0)
            delete(*child)

    reclaim(obj)
}

书举例说update_ptr($ptr, obj)改写成*$ptr = obj, 我理解这只是举了一个例子说明不需要增减计数器。实际后面的代码中可以看出，还是使用的update_ptr($ptr, obj),否则就没有对dec_ref_cnt(obj)的调用了。变化比较大的是dec_ref_cnt(obj函数，它不再递归调用子节点的计数器减量，而是直接把它放到zct结构中，在必要时调用scan_zct, 这就大大减少了计数器值得增减。

• 优点: 延迟了根引用的技术，将垃圾一并回收，减轻了因根引用频发发生的变化导致计数器增减所带来的额外负担。
• 缺点: 失去了引用计数法的一大优点–可即可回收垃圾。另外scan_zct()导致最大暂停时间延长了。

Sticky引用计数法

引用计数法有一个问题就是计数器要设置多大的位宽。如果设置的小了，有可能会出现存不下而溢出的情况；如果设置的大了，又会占用过多的空间。Sticky的思想就是设置一个固定大小的位数，这个位数要比较小，对于溢出的情况下面两种处理方式:

• 什么都不做
  当计数器出现溢出时，不对其进行任何操作，其值就是能存储的最大值，一般情况下这个值很难达到，如果达到了这个值，证明其非常重要，其成为垃圾的可能性也非常小，对其计数不增也不减，不会存在什么大的问题。
• 使用GC标记-清除算法进行管理

  mark_sweep_for_counter_overflow(){
      #所有计数器清零
      reset_all_ref_cnt()
      mark_phase()
      sweep_phase()
  }
  
  #对所有可以达到的节点进行标记，每个节点及其子节点只会进栈一次，所以引用计数的值最多为2， 不会出现溢出的情况
  mark_phase(){
      for(r : $roots)
          #所有根节点放到标记栈中
          push(*r, $mark_stack)
  
      while(is_empty($mark_stack) == FALSE)
          obj = pop($mark_stack)
          #弹出栈，引用计数+1
          obj.ref_cnt++
          #只有引用计数为1才让其子节点进栈，已经进过的不会再进
          if(obj.ref_cnt == 1)
              for(child : children(obj))
                  push(*child, $mark_stack)
  }
  
  #清除节点遍历堆，所有标记位为0的节点进行回收
  sweep_phase(){
      sweeping = $heap_top
      while(sweeping < $head_end)
          if(sweeping.ref_cnt == 0)
              reclaim(sweeping)
          sweeping += sweeping.size
  }

这么做可以在溢出后依然回收，而且没有对循环引用页适用，但是需要重置计数器。查找对象时没有设置标记位，而只是增量计数器，会出现多次查找活动对象的问题。比起一般的GC标记-清除算法需要更多的时间，吞吐量也会变小。

1位引用计数法

1位引用计数法(1 bit Reference Counting)是Sticky引用计数法的极端例子，计数器只有1位大小。这里的计数器不在表示引用的个数，而是表示有一个引用还是多个引用。

1. 当计数器值为0，表示对象引用数为1，这种状态称为UNIQUE
2. 当计数器值为1， 表示引用数为复数, 这种状态称为MULTIPLE

相关伪代码:

#指针复制 
#dest_ptr: 目的指针 
#src_ptr: 源指针 
copy_ptr(dest_ptr, src_ptr){
    #由于目的指针原来指向的内容不再指向，需要对目的指针指向删除操作 
    delete_ptr(dest_ptr)
    #执行复制 
    *dest_ptr = *src_ptr
    #目的指针由于和源指针指向了同一个对象，目的指针需要设置为MULTIPLE 
    set_multiple_tag(dest_ptr)
    #源指针如果原来是UNIQUE, 现在多了一个目的指针，需要设置为MULTIPLE 
    if(tag(src_ptr) == UNIQUE)
        set_multiple_tag(src_ptr)
}

#删除目的指针原来的指向对象 
delete_ptr(ptr){
    #如果原来是UNIQUE，说明对象只有一个指针，删除后需要回收 
    if(tag(ptr) == UNIQUE)
        #回收 
        reclaim(ptr)
}

其过程可以参考下图: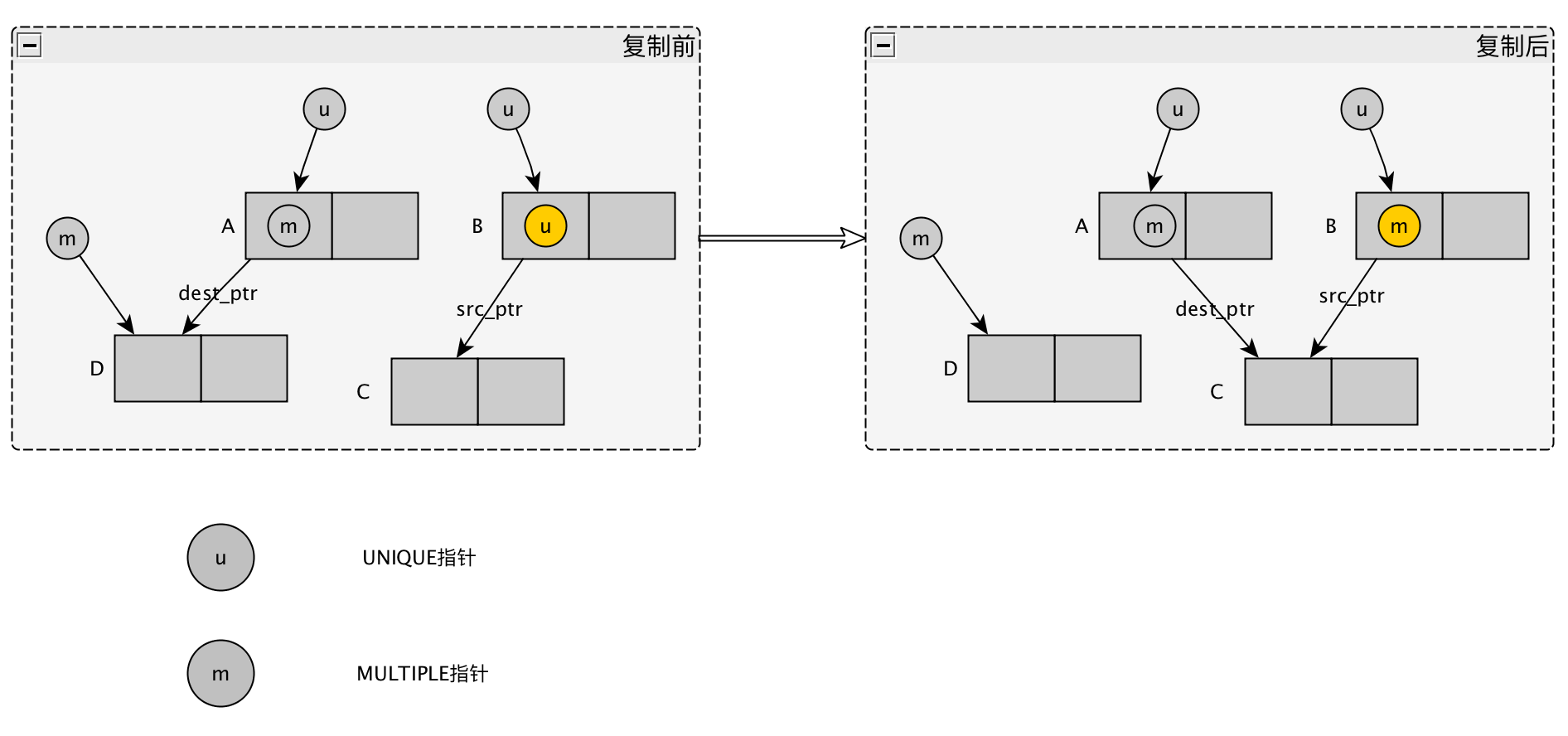

• 优点:
  1. 不容易出现高速缓存缺失， 如上图所示，在更新计数器的时候不需要读取元素的值到内存中（C,D完全没有读), 只需要更新指针的计数器，所以不会出现内存中离得远找出缓存缺失。
  2. 计数器所占空间很小，节省内存。
• 缺点: 1位引用计数器是在大量计数器都不足2的前提下来做的，当出现大量大于2的计数器时，1位引用计数器方法就无法回收这些对象，给堆带来巨大负担。

部分标记-清除算法

部分标记清除法主要是针对之前的无法回收循环引用的缺点而产生的。之前讲的延迟引用计数法可以处理循环引用的情况，但是效率太低。部分-标记清除算法只针对有可能是循环引用的对象上执行，在一般的对象上还是执行引用计数法。下面结合代码图图示说明一下部分标记-清除算法的过程。

部分标记-清除算法中，对象被涂成四种颜色来管理。每个颜色的含义如下：

1. 黑(BLACK): 绝对不是垃圾的对象(对象产生时的初始颜色)
2. 白(WHITE): 绝对是垃圾的对象
3. 灰(GRAY): 搜索完毕的对象
4. 阴影(HATCH): 可能是循环垃圾的对象

首先我们假设有一个循环引用对象群，初始状态如下：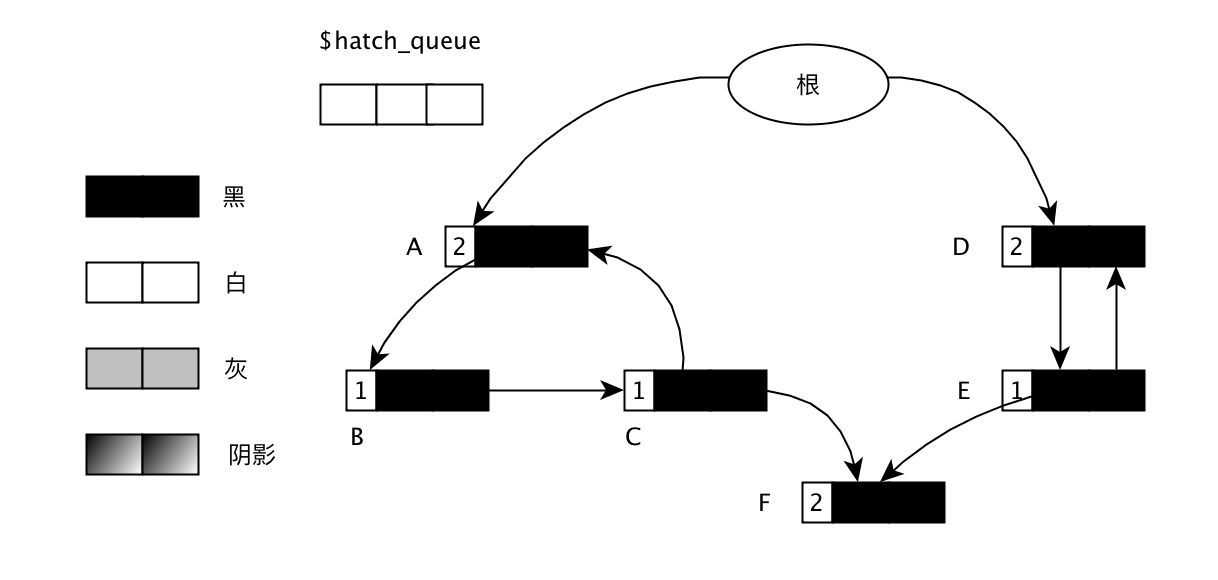

图中A和D是由根引用。所有对象在初始状态下都为黑色。
对应的初始代码如下:

new_obj(size){
    obj = pickup_chunk(size)
    if(obj != NULL)
        #初始颜色会BLACK
        obj.color = BLACK
        obj.ref_cnt = 1
        return obj
    else if(is_empty($hatch_queue) == FALSE)
        #当空间不够用时扫描可能是循环引用的对象，然后释放出新的空间, 再次调用new_obj
        scan_hatch_queue()
        return new_obj(size)
    else
        allocation_fail()
}

当执行dec_ref_cnt()时, 引用计数为0， 则回收。不为0时都认为是可能存在循环引用的对象, 都标记成HATCH, 并且把这个对象放到$hatch_queue当中。代码如下:

dec_ref_cnt(obj){
    obj.ref_cnt--
    #ref_cnt == 0, 回收对象
    if(obj.ref_cnt == 0)
        delete(obj)
    #ref_cnt != 0 认为是可能存在循环引用的对象
    else if(obj.color != HATCH)
        obj.color = HATCH
    enqueue(obj, $hatch_queue)
}

针对上面的图，如果A的引用被删除了，则执行dec_ref_cnt()之后的状态如下图:

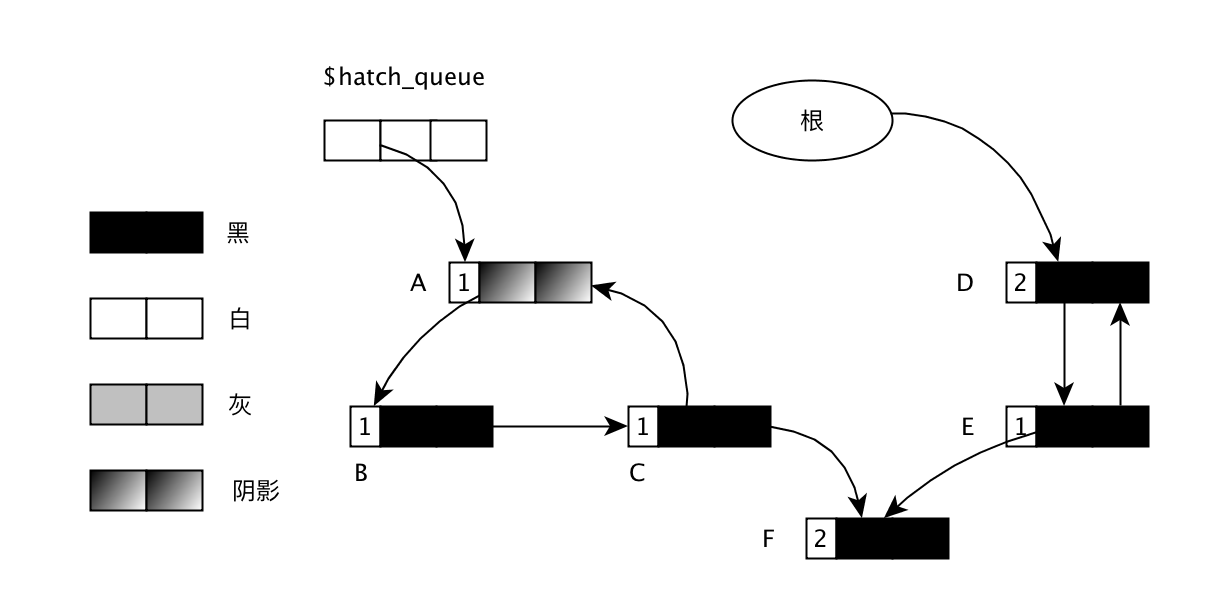
这是对象群在调用new_obj()时已经没有心的内存空间可以使用，所以会触发scan_hatch_queue()函数的调用。对应代码如下:

scan_hatch_queue(){
    #可能是循环引用的对象出队列
    obj = dequeue($hatch_queue)
    #如果颜色为HATCH, 依次调用下面的函数
    if(obj.color == HATCH)
        paint_gray(obj)
        scan_gray(obj)
        collect_white(obj)
    ##如果颜色不为HATCH, 证明不是循环引用对象，继续下一个元素
    else if(is_empty($hatch_queue) == FALSE)
        scan_hatch_queue()
}

上面需要调用的paint_gray(obj)函数主要作用是深度遍历对象，搜索过的对象标记位GRAY:

paint_gray(){
    #对原来是BLACK或HATCH的对象标记为GRAY
    if(obj.color == (BLACK | HATCH))
        obj.color = GRAY
    #深度遍历子节点，引用计数减量, 递归调用paint_gray记性标记
    for(child : children(obj))
        (*child).ref_cnt--
        paint_gray(*child)
}

执行完上面的函数后，对象的状态如下图: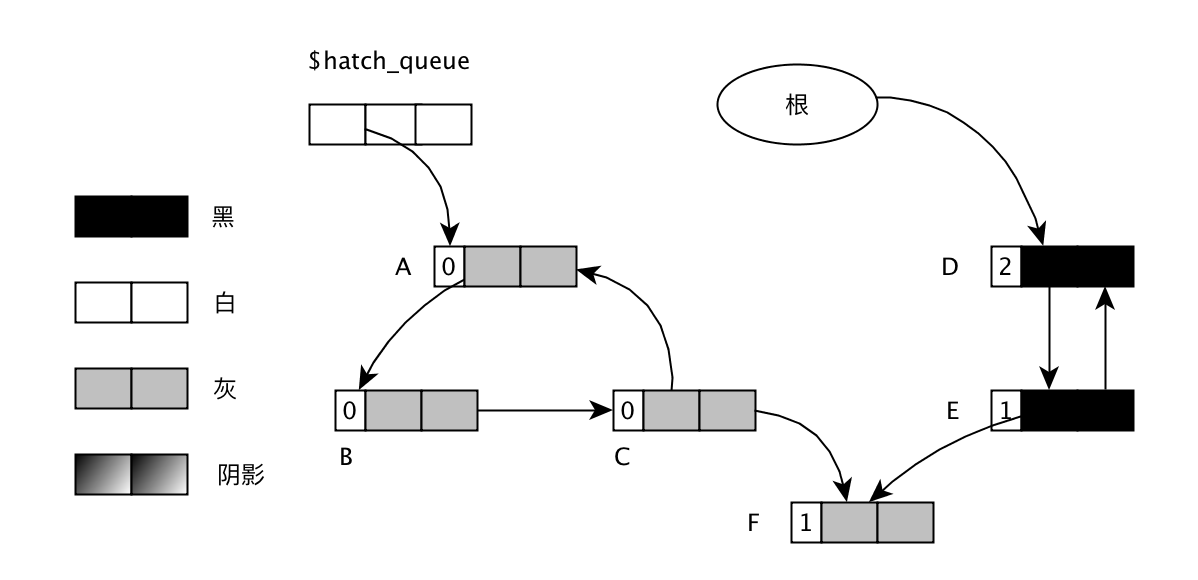

下面scan_gray(obj)的目的是扫描刚才的GRAY节点，把其中的垃圾对象找出来，标记成WHITE:

scan_gray(obj){
    if(obj.color == GRAY)
        if(obj.ref_cnt > 0)
            #ref_cnt>0, 不是垃圾，需要标记成BLACK
            paint_black(obj)
            #ref_cnt == 0, 是垃圾对象，标记成WHITE
        else
            obj.color = WHITE
            for(child : children(obj))
                scan_gray(*child)
}

paint_black(obj){
    obj.color = BLACK
    for(child : chidren(obj))
        #由于执行paint_gray的时候ref_cnt--, 这里要恢复ref_cnt
        (*child).ref_cnt++
        if((*child).color != BLACK)
            paint_black(*child)
}

标记后的对象如下: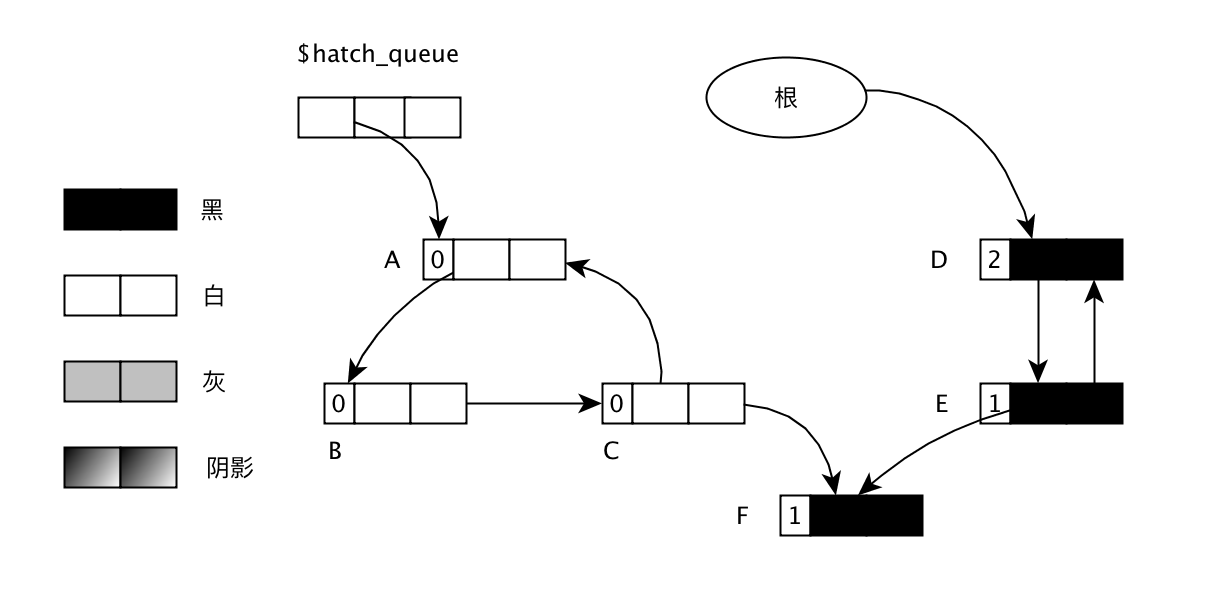

到上面的步骤后，可以看出已经知道那些颜色为WHITE的对象就是垃圾对象，这些对象需要回收，回收代码入下:

collect_white(){
    if(obj.color == WHITE)
        obj.color = BLACK
        for(child : children(obj))
            collect_white(*child)
        reclaim(obj)
}

回收后的图如下: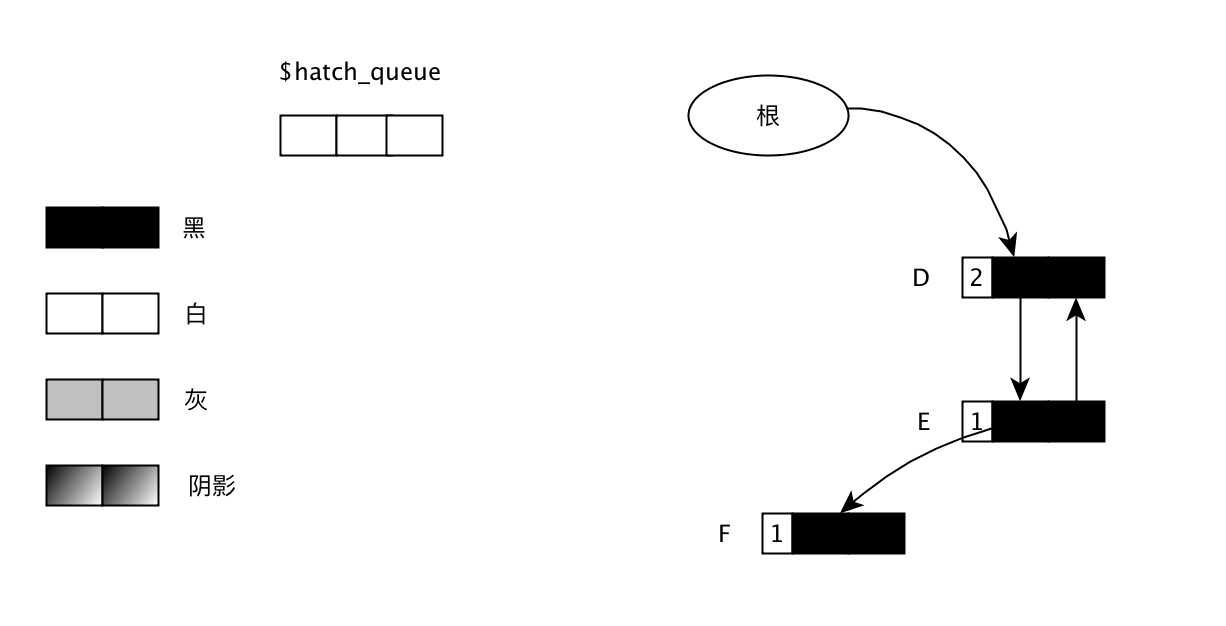

上面就是部分标记-清除算法的过程。这个算法的优点就是，只搜索可能是循环垃圾的对象群，就是阴影部分，如何确定这个范围呢？首先产生垃圾循环的条件有两个:

1. 产生循环引用。
2. 删除从外部到循环引用的引用。

部分标记-清除算法就利用dec_ref_cnt()函数来判断，如果引用计数减值后不为0， 那这个对象有可能就是循环对象的一份子。
这个算法的缺点就是需要三次查找对象，而每次查找的数量不少，所以付出的成本比较大。

GC复制算法

GC复制算法把原来的内存空间分为两部分(From空间和To空间), 当From空间不够分配时，就会执行GC复制算法，把From空间的活动对象复制到To空间，复制完成后交换From和To空间，GC结束，分配时去心的From空间查找。

copying(){
    #$to_start To空间的起始地址
    #$free 要copy到的起始地址
    $free = $to_start
    for(r : $roots)
        *r = copy(*r)
    #交换From 和 To 空间
    swap($from_start, $to_start)
}

#执行From 到 To 的 copy
copy(obj){
    # 如果obj.tag != COPIED, 此对象还没有被执行过COPY, 对其执行COPY
    if(obj.tag != COPIED)
        copy_data($free, obj, obj.size)
        #执行完后改变tag值，下次不再对其执行COPY
        obj.tag = COPIED
        #forwarding是原来对象指向复制后的对象的指针，便于新老节点对应起来，下面递归查询的时候好查找
        obj.forwarding = $free
        #free是要复制到的起始地址，当复制完一个对象后，需要前进size, 到达新的地址(To空间空闲的起始地址)
        $free += obj.size
        
        #对执行过的对象执行深度遍历，全部活动子节点都COPY到TO空间
        for(child : children(obj.forwarding))
            *child = copy(*child)
    #注意，当对根节点的元素执行时，返回的是根节点执行的obj.forwarding, 
    #所以全部执行完后，根节点结合就是原来的根节点集合的forwarding指针指向的元素
    return obj.forwarding
}

new_obj(){
    #这里FROM和TO等分，如果空间不够，执行GC
    if($free + size > $from_start + HEAP_SIZE/2)
        copying()
        #执行完GC后空间还不够，返回失败
        if($free + size > $from_start + HEAM_SIZE/2)
            allocation_fail()

    obj = $free
    obj.size = size
    $free += size
    return obj
}

GC复制算法过程参考下面的图: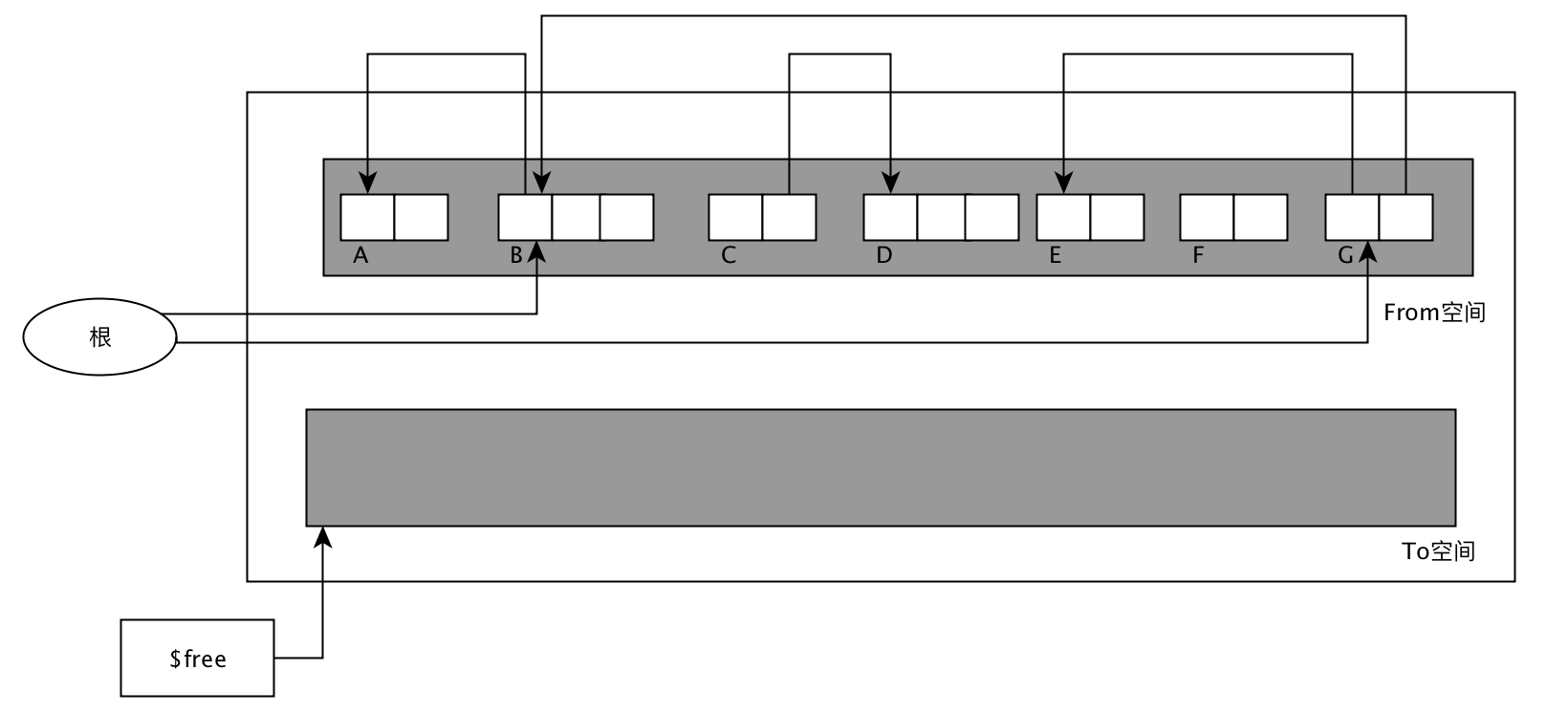

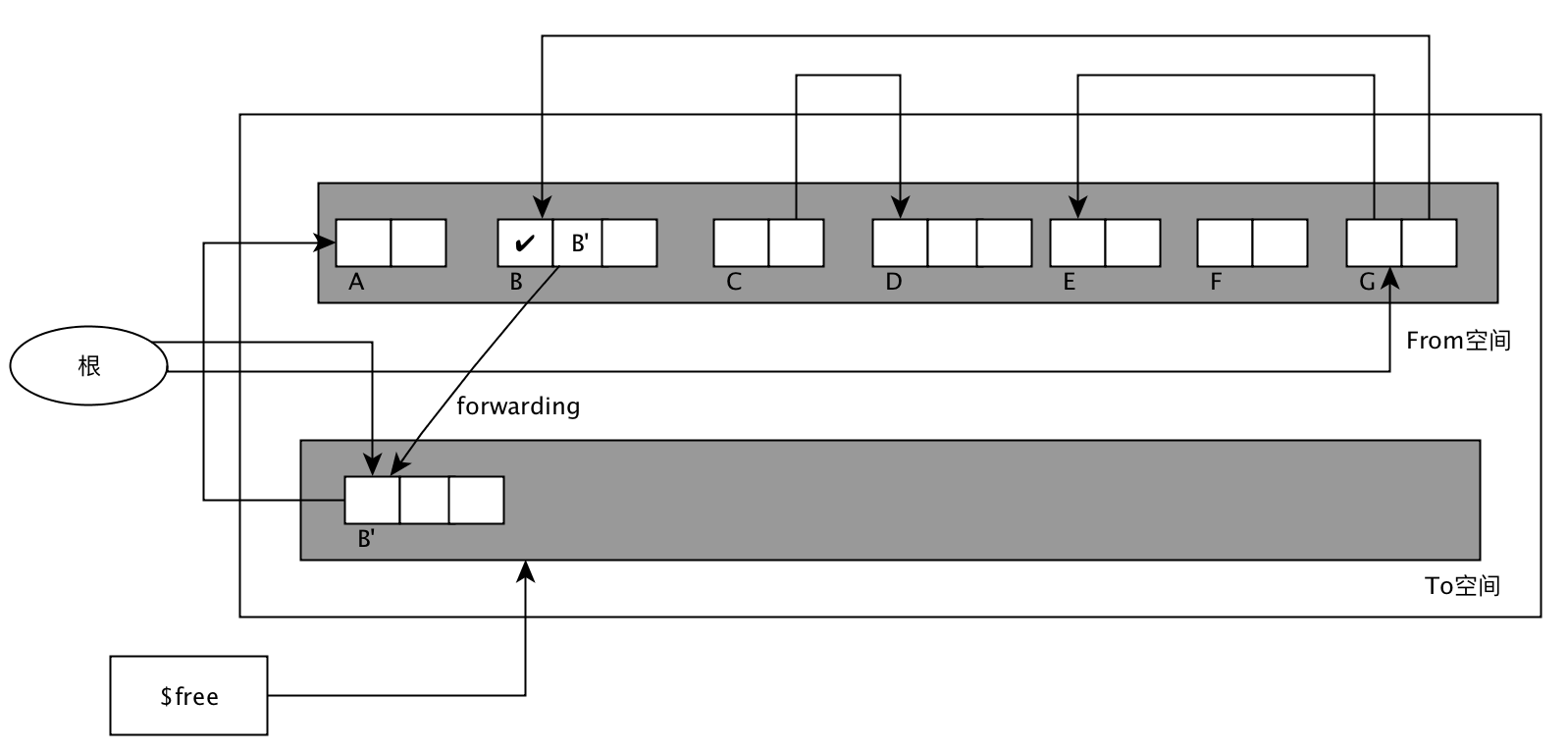
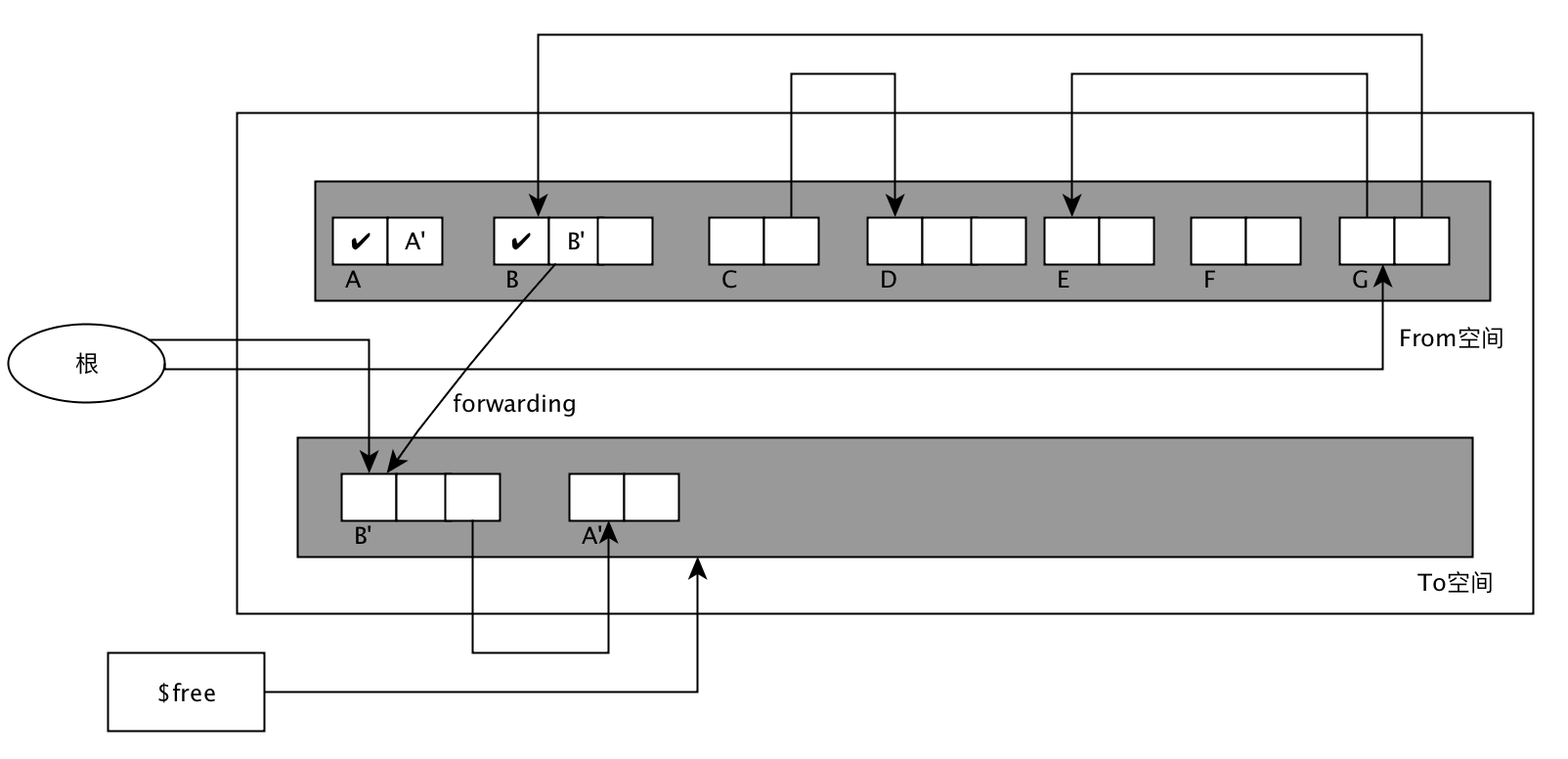
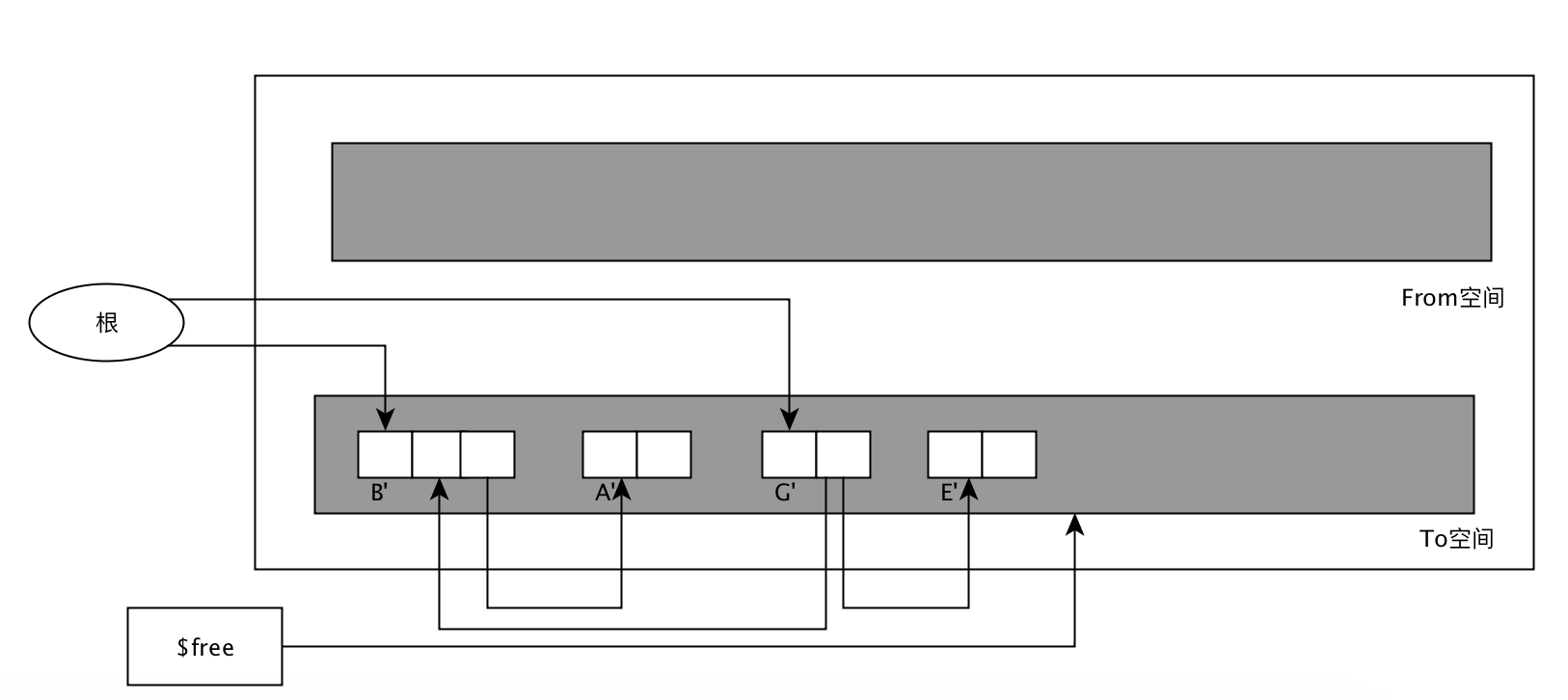
• 优点:

1. 优秀的吞吐量: 只需要搜索活动对象，不需要其他的搜索。
2. 可实现高速分配: 不需要空闲链表，只移动$free指针，快速分配。
3. 不会发生碎片化: 因为分配的都是连续的，GC之后也是连续的，对象都放在了堆的一端(叫做压缩)。
4. 与缓存兼容: 深度优先遍历，关联的节点都被放到了相邻的位置。

• 缺点:

1. 堆使用效率低下: GC复制算法通常把堆分为二等分，只有一半可以来安排对象。
2. 不兼容保守式GC算法: 会发生对象的移动。
3. 递归调动函数: 递归复制，每次调用都会消耗栈，会有栈溢出的可能。

Cheney的GC复制算法

上面提到GC复制算法用递归复制，会有栈溢出的可能。Cheney的GC复制算法则采用广度优先的方式，用循环代替递归，解决栈溢出的问题。

copying(){
    scan = $free = $to_start
    for(r : $roots)
        *r = copy(r)
    #广度优先遍历需要一个队列保，scan 到 $free 就是这个隐藏的队列
    while(scan != $free)
        for(child : children(scan))
            *child = copy(*child)
        scan += scan.size
        
    swap($from_start, $to_start)
}

copy(){
    #如果obj.forwarding是指向To空间指针则返回TRUE, 如果不是则返回FALSE
    if(is_pointer_to_heap(obj.forwarding, $to_start) == FALSE)
        copy_data($free, obj, obj.size)
        obj.forwarding = $free
        $free += obj.size
    return obj.forwarding
}

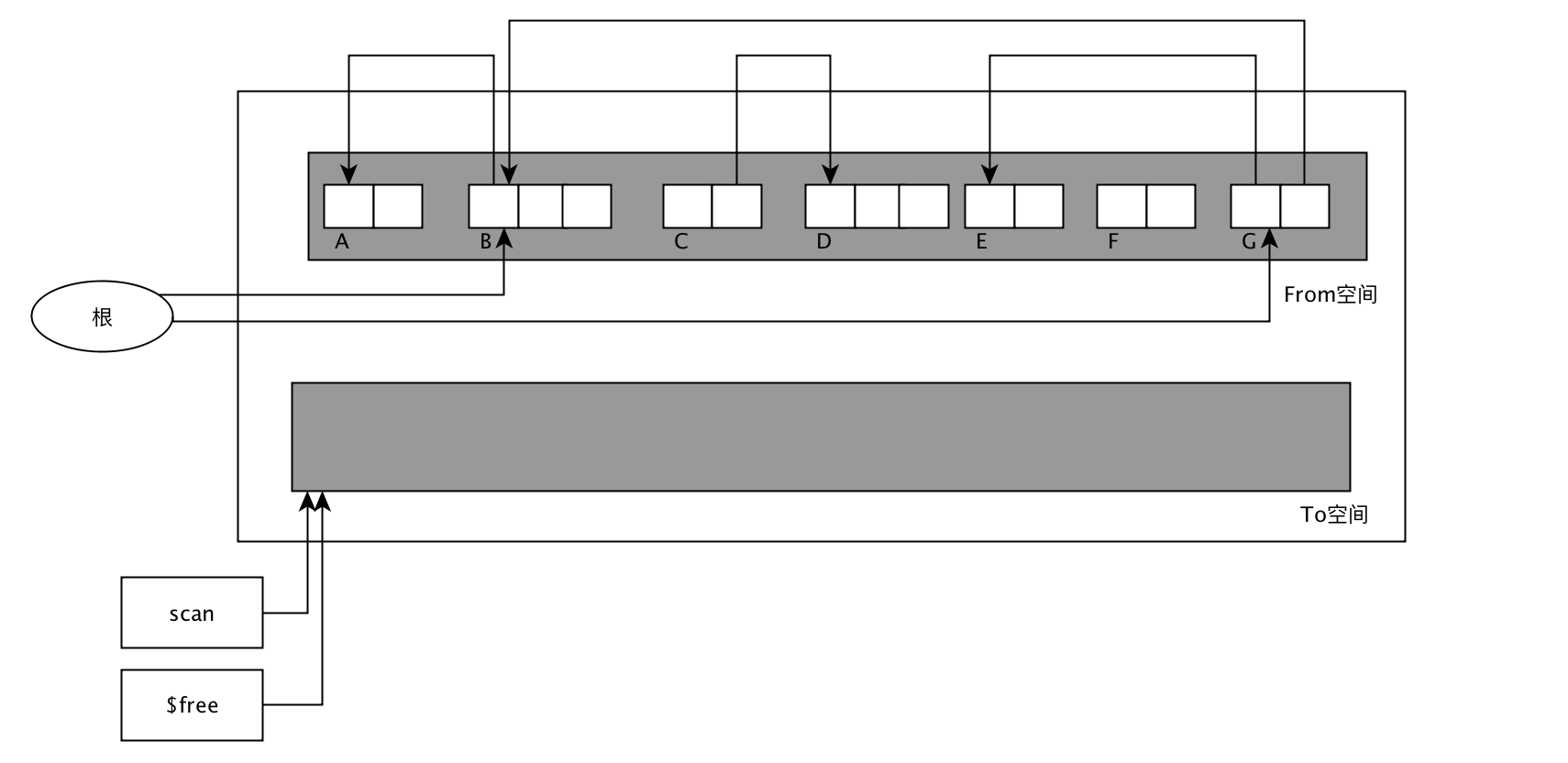
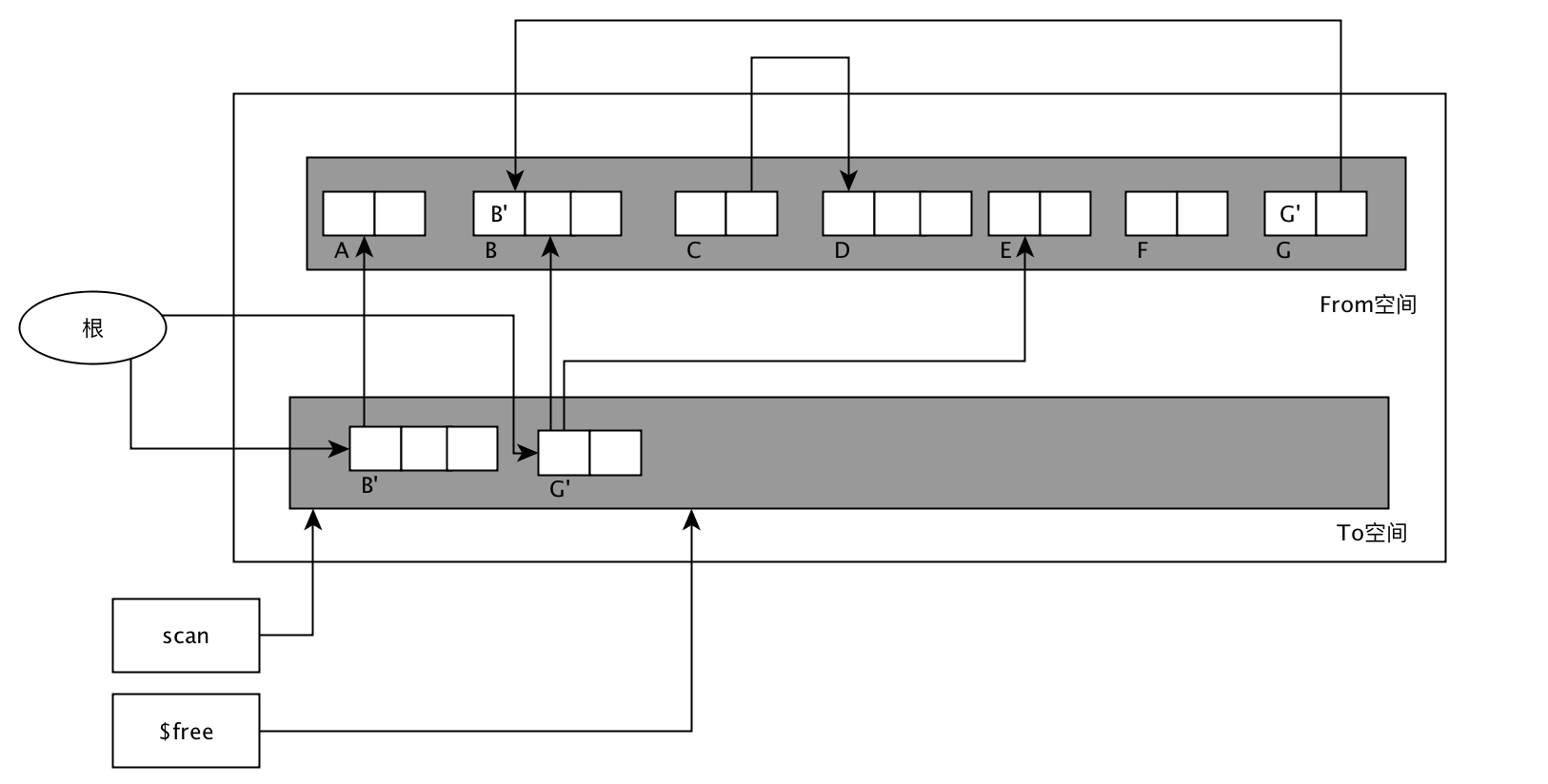
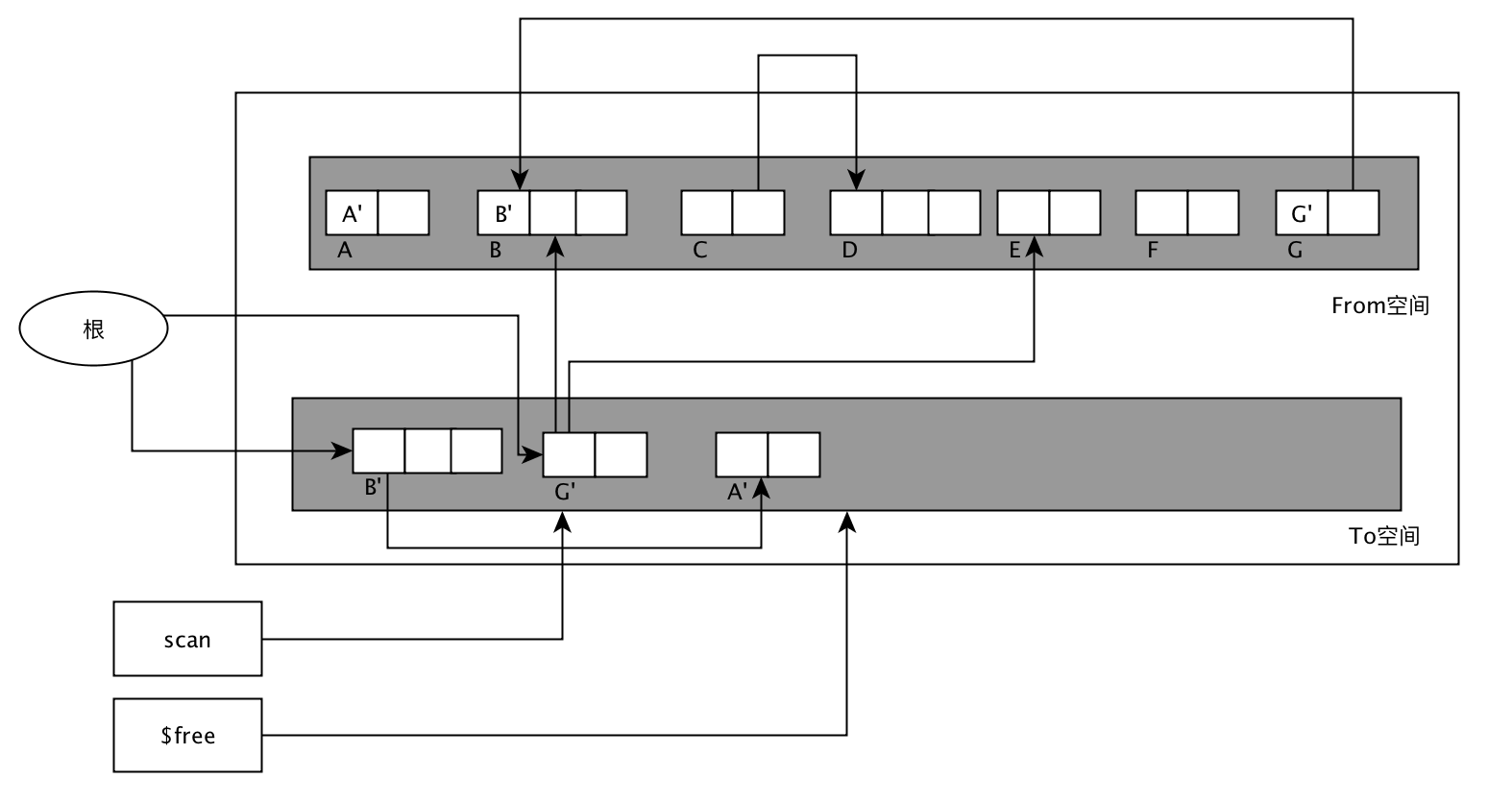
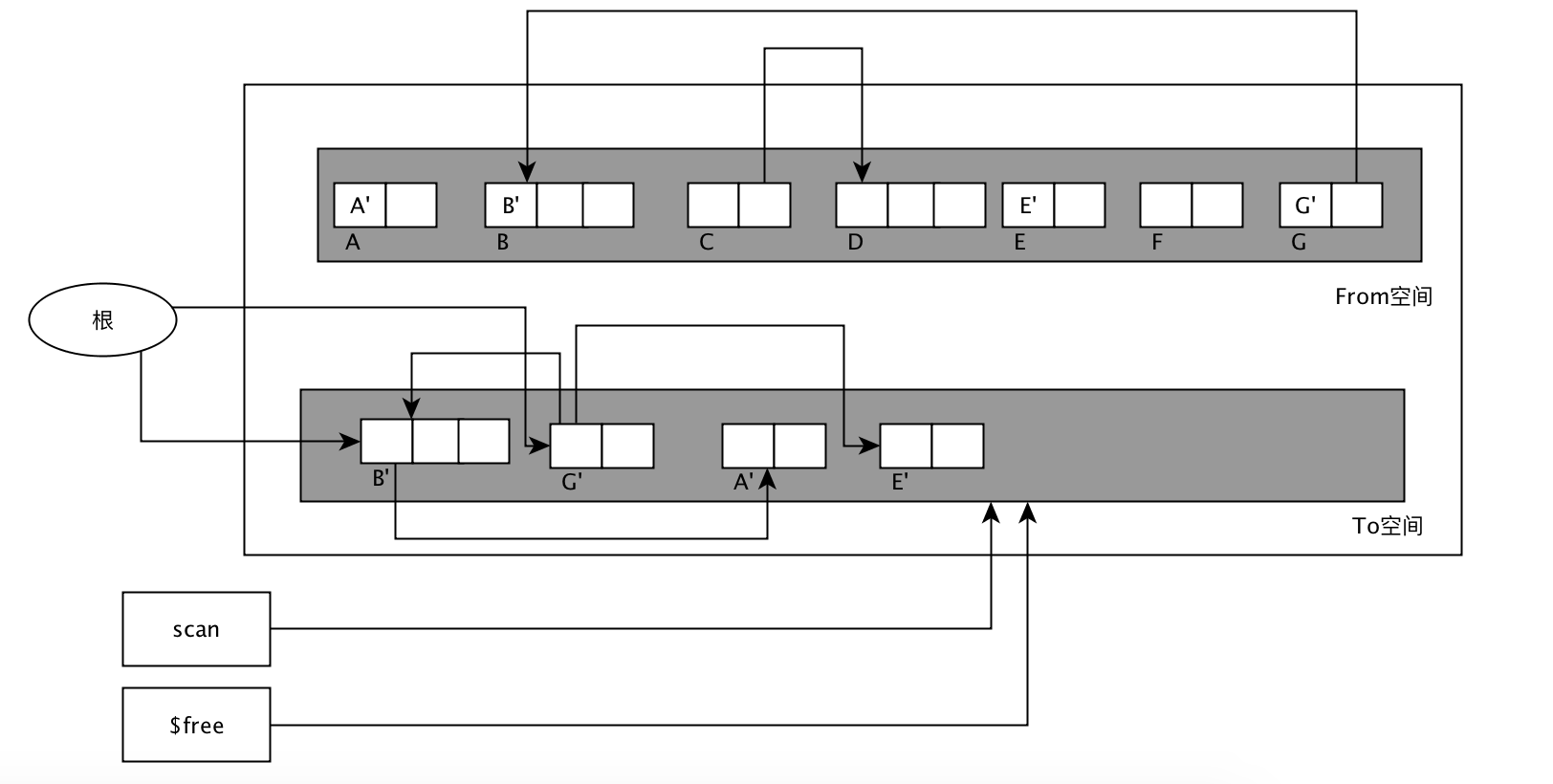
这个算法的缺点是不能利用局部缓存，因为有关系的节点不是相邻的。

近似深度优先搜索方法

为了解决Cheney算法不能利用局部缓存，这里进行了一个改进，对于每个“页面”内部都是广度优先搜索。下面通过一个例子，看一下Cheney与近似深度优先搜索的方法对比:
图1，原始的引用关系: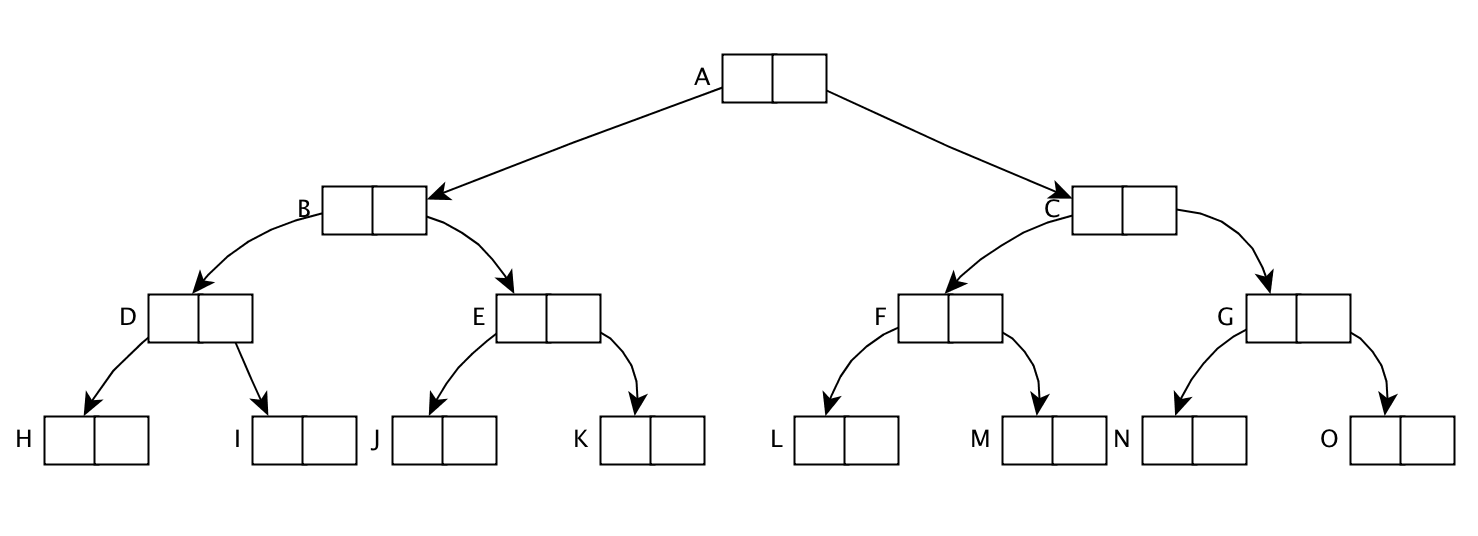

图2，假设每三个节点占用一个”页面”的空间，下面就是Cheney方法，广度优先遍历后的ji结果: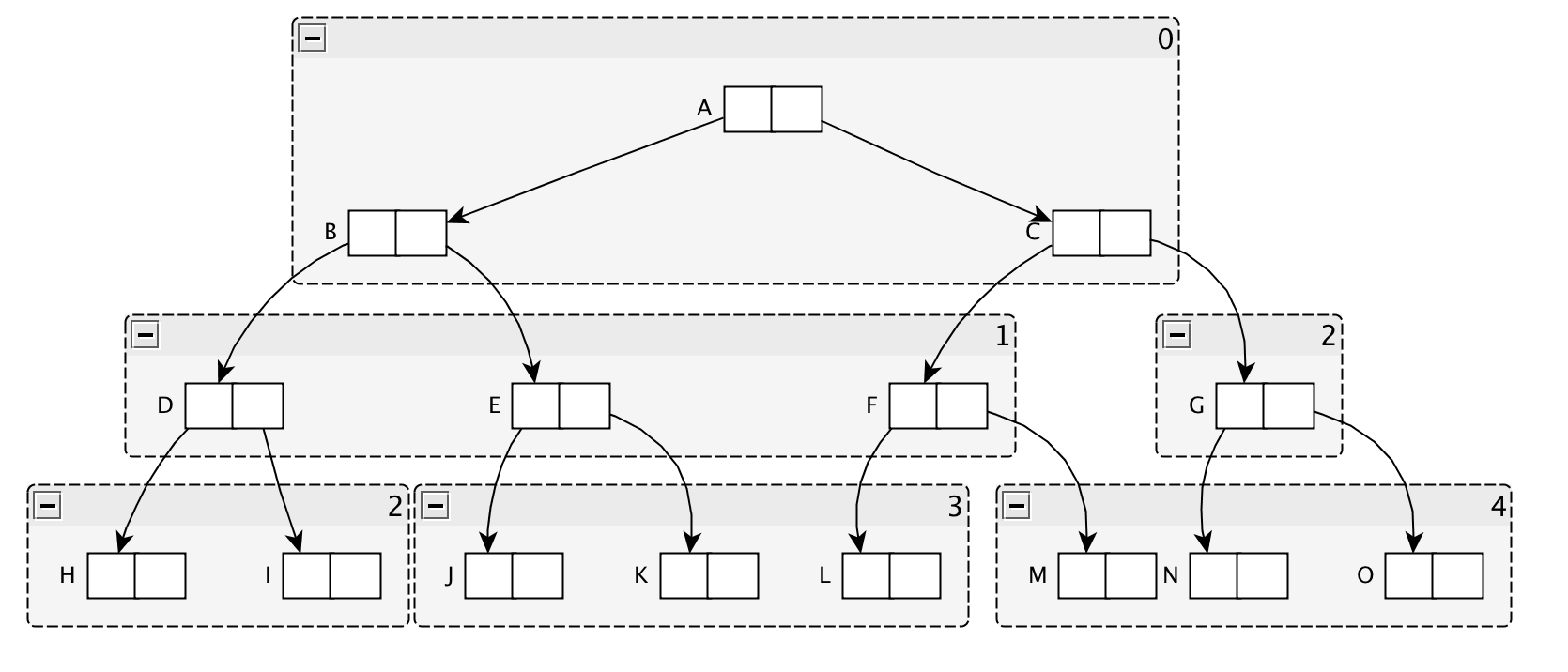

可以看出，上图中相互引用的节点之间存储的比较分散，不容里利用局部缓存。
图3是利用近似深度优先搜索方法后的结果，可以看出分布比较集中，可以很好利用局部缓存。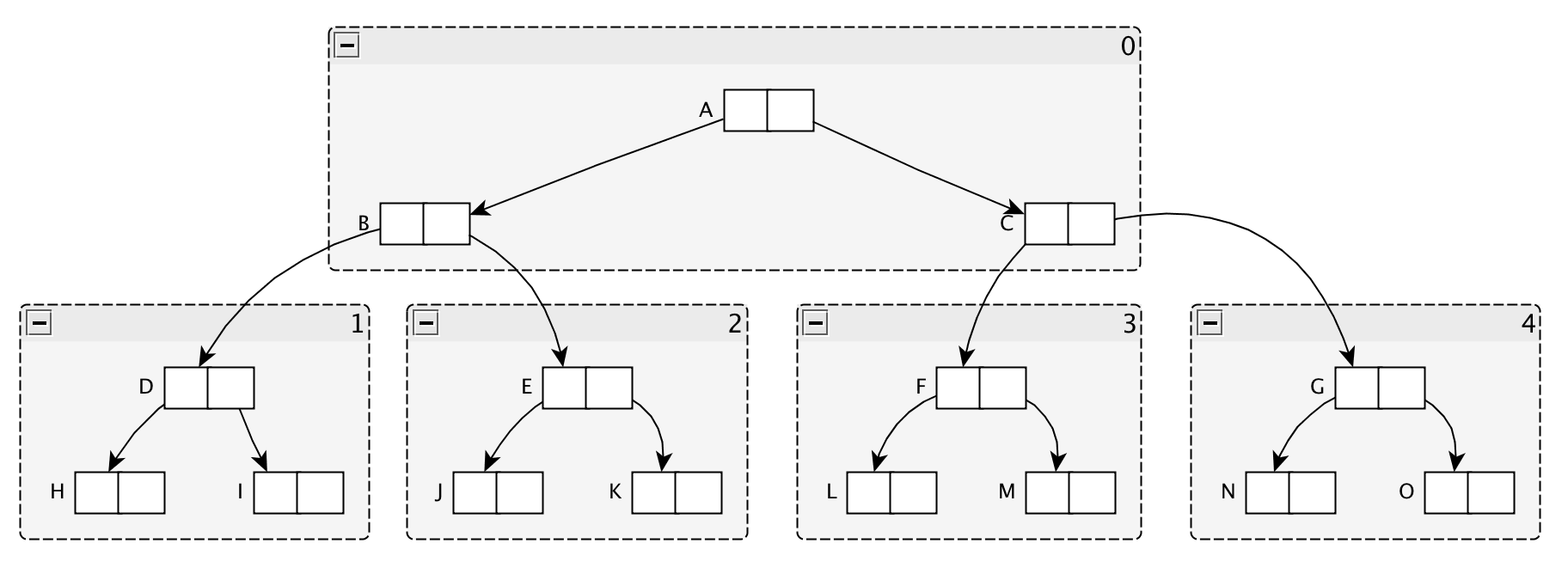

多空间复制算法

上面降到复制算法的一个明显的特征就是堆的利用率低。为了改善这个问题，多空间复制的算法的思想就是把一个堆N等分，只对其中2块空间执行GC复制算法，对剩下的(N-2)块空间执行GC标记-清除算法，也就是把这两种算法组合起来使用。具体细节不再展开。这个方法的优点是可以更有效的利用堆，但是缺点也很明显，就是标记-清除算法的缺点:分配耗费时间，分块碎片化等。

总结

基本算法是进行GC的基本思想，每个算法都有其缺点和优点，没有算法能够完美解决所有问题。所以后面的算法利用这几种基本算法的组合和变形，更好的提高GC的性能。