oohcode

$\bigodot\bigodot^H \rightarrow CODE$

垃圾回收进阶算法

了解GC的基本算法后，还需要了解各种改进的GC算法，这些算法是在之前的基础上进行扩展和组合的。主要包括GC标记-压缩算法, 保守式GC, 分代垃圾回收， 增量式垃圾回收和RC Immix算法等。

GC标记-压缩算法

GC标记-压缩算法(Mark Compact GC)是将GC标记-清除算法与GC复制算法相结合的产物。 GC标记-压缩算法由标记阶段和压缩阶段构成。标记阶段和GC标记-清除算法提到的标记阶段一样。接下来需要搜索数次的堆来进行压缩。压缩阶段通过数次搜索堆来重新装填活动对象。

Lisp2算法

标记阶段的代码就不重复了，这里主要看压缩阶段的代码，下面可以看出压缩阶段主要分为三个步骤:

  1. 第一步是set_forwarding_ptr, 主要是按顺序遍历堆内的活动对象，每个活动对象的forwarding指针指向的是以后这个活动对象需要移动到的位置。
  2. 第二步是adjust_ptr, 遍历整个活动对象，复制他们之间的引用关系, 这个步骤只更新指针。
  3. 第三步move_obj, 遍历整个堆，对活动对象进行移动。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
compaction_phase() {
    set_forwarding_ptr()
    adjust_ptr()
    move_obj()
}

set_forwarding_ptr() {
    scan = new_address = $head_start
    while(scan < $head_end)
        # 对被标记的对象，forwarding指针指向应该移动到的位置
        if(scan.mark == TRUE)
            scan.forwarding = new_address
            new_address += scan.size
        # 遍历整个堆
        scan += scan.size
}

adjust_ptr() {
    # 移动根指针
    for(r : $roots)
        *r = (*r).forwarding
    
    scan = $head_start
    while(scan < $head_end)
        # 每个活动对象，原来指向子节点的指针改为指向直接点的forwarding指向的地址
        if(scan.mark == TRUE)
            for(child : children(scan))
                *child = (*child).forwarding
        scan += scan.size
}


move_obj() {
    scan = $free = $head_start
    # 遍历堆
    while(scan < $head_end) 
        if(scan.mark == TRUE)
            new_address = scan.forwarding
            # 移动当前对象到对象forwarding指针指向的地址
            copy_data(new_address, scan, scan.size)
            # 移动完活动对象后清空指针和标记，防止再次移动
            new_address.forwarding = NULL
            new_address.mark = FALSE
            # $free最终是压缩后可分配空间的开始
            $free += new_address.size
            scan += scan.size
}

上面的步骤可以用下面的图形化的例子来描述:
首先假设原始状态如下: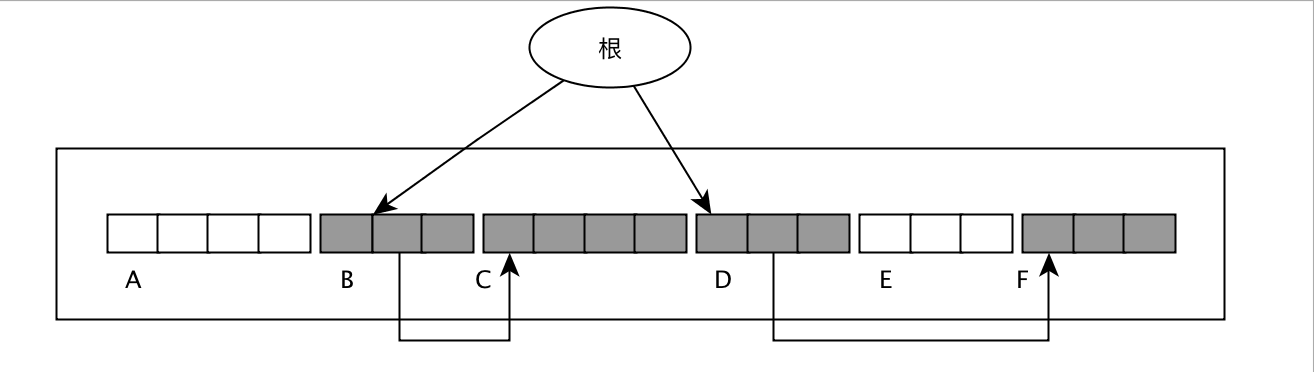
原始状态
先对其进行标记: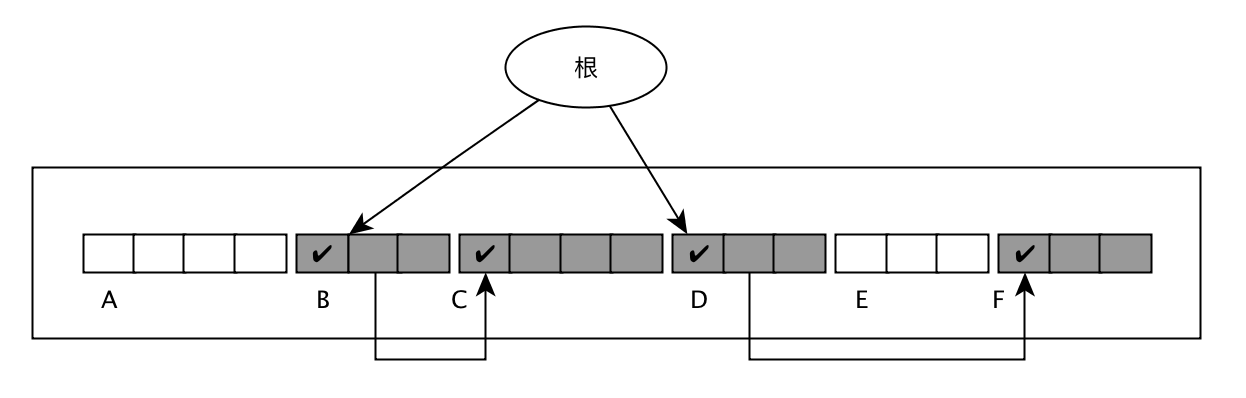
标记后
设定forwarding指针:
设定forwarding指针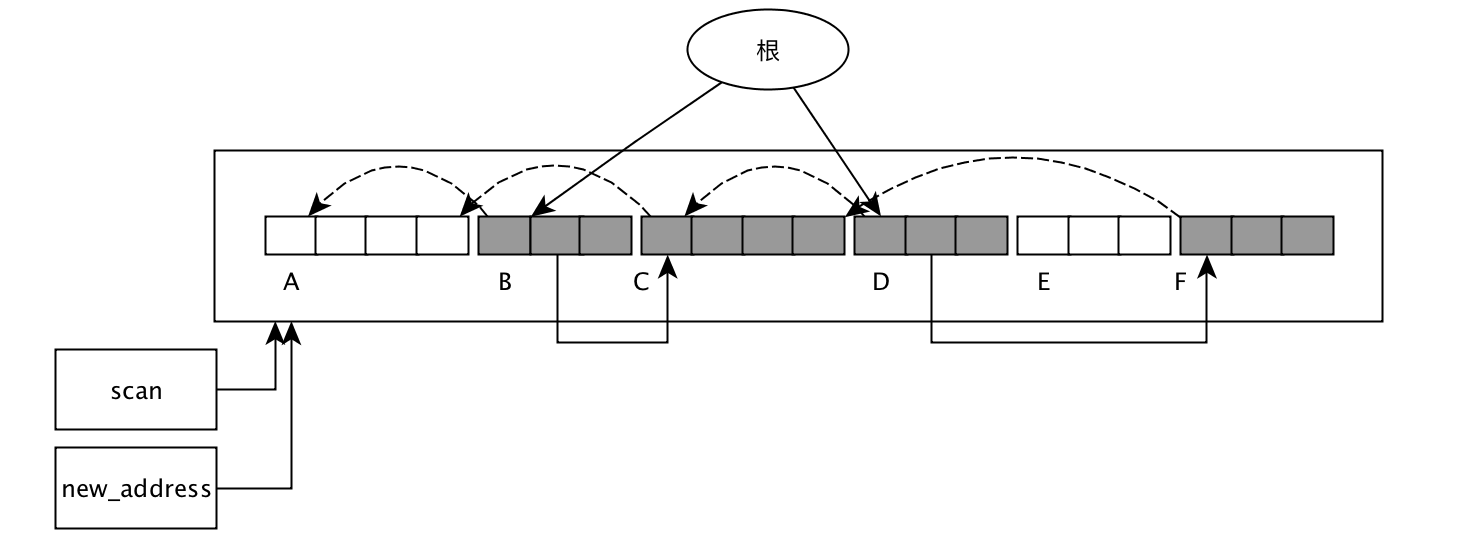
更新指针:
更新指针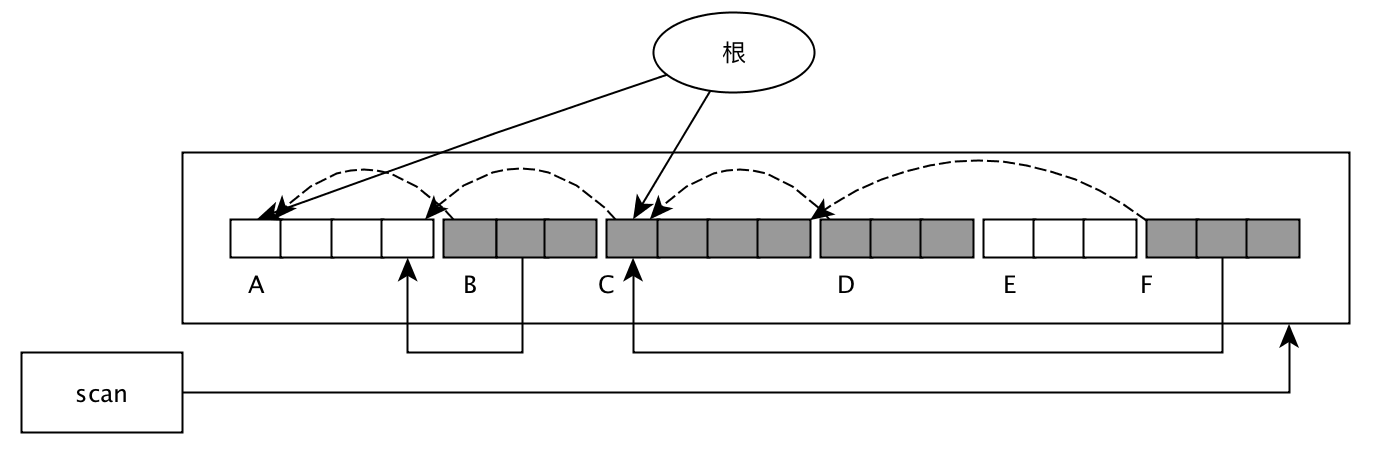
移动对象:
移动对象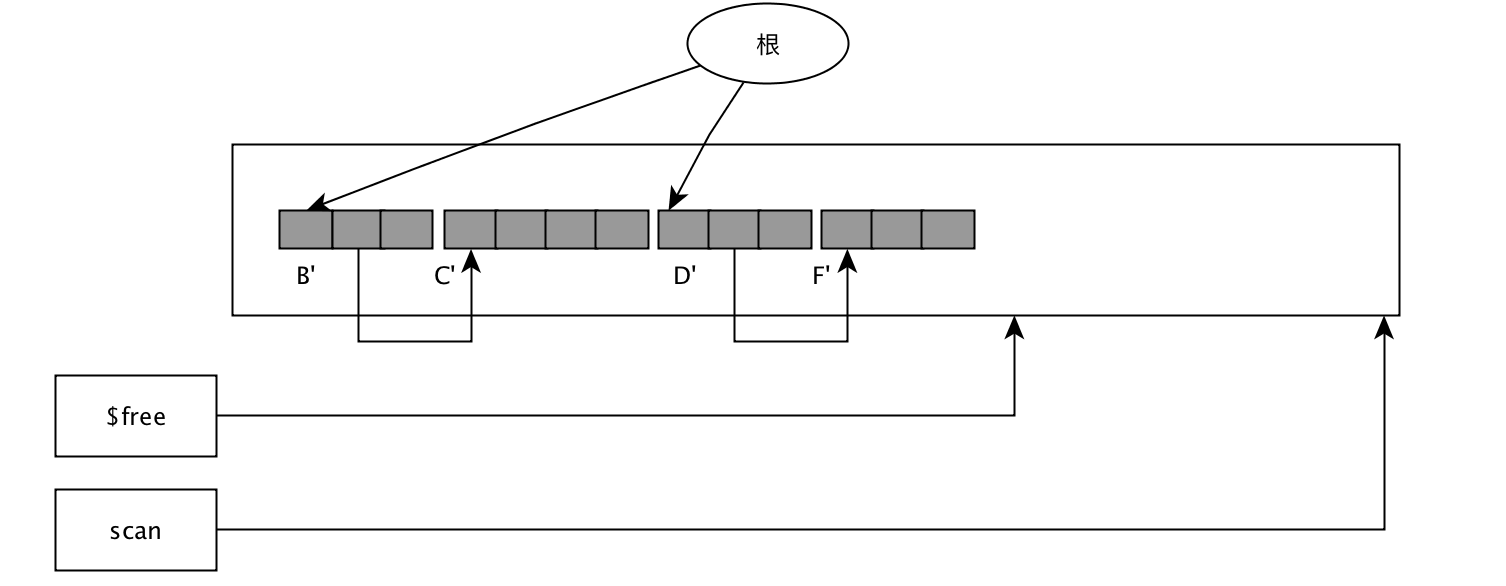
上面可以看出，整个过程只是把活动对象往一边移动，活动对象之间的顺序不变。

  • 优点: 这个算法相对其他算法而言，堆利用率高，而且所有活动对象压缩到一端，不存在碎片化，能够充分的利用堆。
  • 缺点: 整个压缩过程需要3遍对堆的搜索，也就是执行该算法所花费的时间与堆大小成正比，吞吐量要劣于其他算法。

Two-Finger算法

Two-Finger算法由两个步骤构成:

  1. 移动对象
  2. 更新指针

我们知道Lisp2算法是把所有对象向右滑动，不改变活动对象的顺序，而Two-Finger算法则是真正的移动对象，把后面的活动对象移动到前面的空间。为了防止对象相互覆盖，必须要将所有对象整理成大小一致, 这个该算法的一个前提条件。另外Lisp2算法需要单独设置forwarding指针，但是Two-Finger算法可以利用对象的域来设定forwarding指针，不要单独占空间。
两个步骤对象的伪代码如下, 要说明的是move_obj函数有两个指针:$free, 从头往后找，找空闲的空间； live，从后往前找，找活动对象。这两个指针就是Two-Finger的名称由来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
move_obj() {
    #从头开始找空闲空间
    $free = $heap_start
    #从尾开始找活动对象
    live = $heap_end - OBJ_SIZE
    while(TRUE)
        #free, 是活动对像就略过,继续往后找
        while($free.mark == TRUE)
            $free += OBJ_SIZE
        #live, 是活动对象就略过，继续往前找
        while(live.mark == FALSE)
            live -= OBJ_SIZE
        # free 指针 比 live小，证明还没有结束，否则证明查找结束了
        if($free < live)
            #把live指向的对象复制到free地址
            copy_data($free, live, OBJ_SIZE)
            #live指向的对象的forwarding指针指向新地址，为下一步更新指针做准备
            live.forwarding = $free
            #移动过的对象标记位FALSE
            live.mark = FALSE
        else
            break
}

adjust_ptr() {
    for(r : $roots)
        #*r>=$free的条件是对于被移动过的对象执行指针更新，没有移动过的对象保持原样
        if(*r >= $free)
            *r = (*r).forwarding
        
    scan = $head_start
    #scan < $free 是因为对于大于scan的节点已经失效，只对当前活动对象更新
    while(scan < $free)
        #更新过的标记一下
        scan.mark = FLASE
        for(child : children(scan))
            #*child >= $free 的条件是对于被移动过的对象执行指针更新，
            # 没有移动过的对象保持原样
            if(*child >= $free)
                *child = (*child).forwarding
        scan += OBJ_SIZE
}
  • 优点: 不需要额外的内存存储forwarding指针，内存使用效率比Lisp2高，只搜索两次堆，吞吐量也更好.
  • 缺点: 压缩后对象的顺序发生了很大变化，不利于缓存的使用。而且每个对象大小必须一致，限制比较多。

表格算法

表格算法是综合了Lisp2和Two-Finger两种算法优点的算法。其主要步骤也是有两部分:

  1. 移动对象(群)以及构筑间隙表格(break table)
  2. 更新指针

前面两个每次都是移动一个活动对象，而在表格算法种每次移动的是一个群连续的活动对象，更新指针所有的信息也不再是forwarding指针，而是是有个一个叫间隙表格的方法。间隙表是由两个值组成的，其中每个表格代表的是一个活动对象群的入口，左值代表活动对象群的首地址，右值代表活动对象群所相邻的前面的空间占分块的总大小。
第一步过程可以用伪代码来表示:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
movie_obj(){
    #从头开始遍历
    scan = $free = $heap_start
    size = 0
    while(scan < $head_end)
        while(scan.mark == FLASE)
            # size 记录相邻的非活动对象的大小
            size += scan.size
            scan += scan.size
        # 记录活动对象的首地址
        live = scan
        while(scan.mark == TRUE)
            scan += scan.size
        # 上面两个while后，找到了第一个连续的非活动空间和第一个连续的活动空间
        # 移动活动对象群，并构筑间隙表格
        slide_objs_and_make_bt(scan, $free, live, size)
        # 移动后记录下一个空闲空间地址
        $free += (scan -live)
}

slide_objs_and_make_bt函数是一个比较复杂的过程，它主要由两部分组成:

  1. 移动对象群
  2. 移动间隙表格

可以用下面的图表示:
首先执行完上面代码到slide_objs_and_make_bt之前: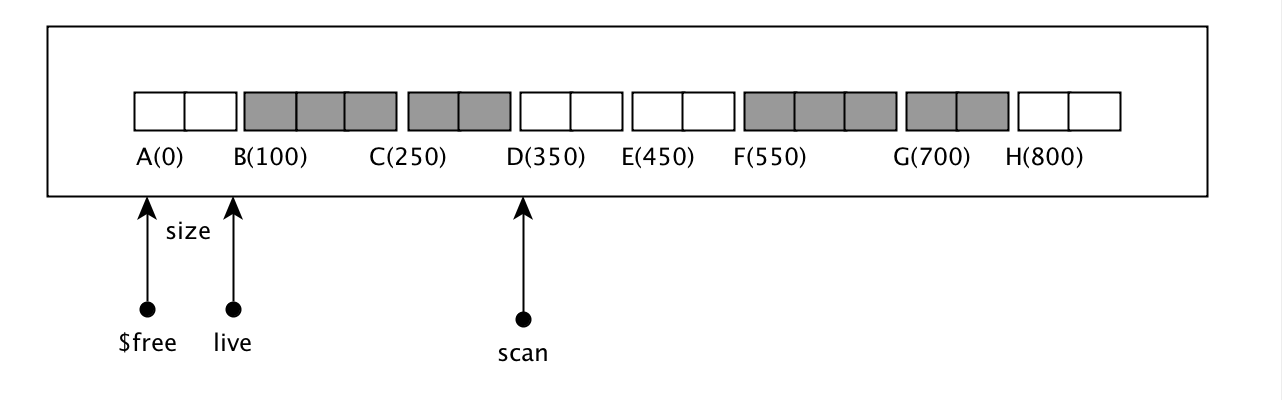
间隙表格
执行slide_objs_and_make_bt后, 移动了对象群，并且在空出来的空间里记录了间隙表格, 左值100表示对象群首地址B的地址，右值100表示B之前的空白块长度为100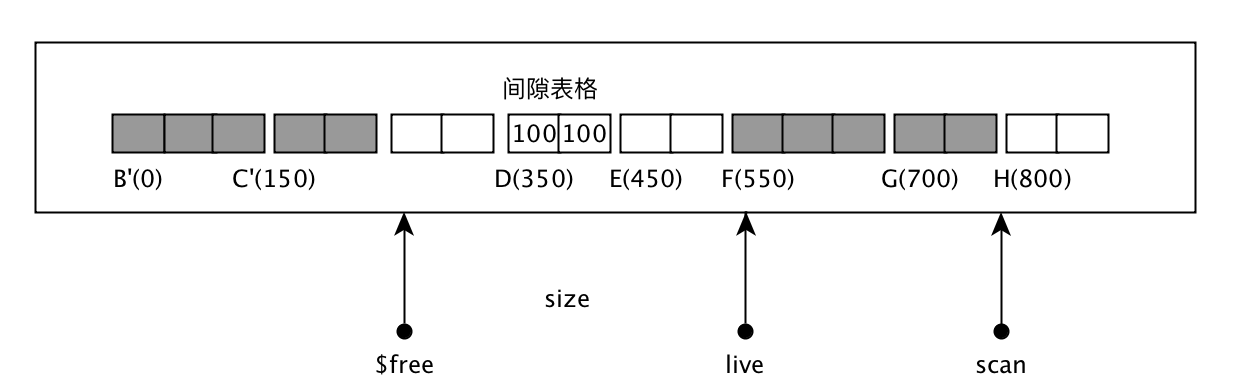
间隙表格
再次执行slide_objs_and_make_bt后，F开头的对象群也进行了移动，并且把两个活动对象群对应的间隙表格都放到了空白块中，第二个间隙表格的550表示F的起始地址，右值300表示第一次执行slide_objs_and_make_bt后，第一个活动对象群的末尾到第二个活动对象群的开始，正好是6块，也就是上图$free到live的size大小是300。执行完最终结果如下: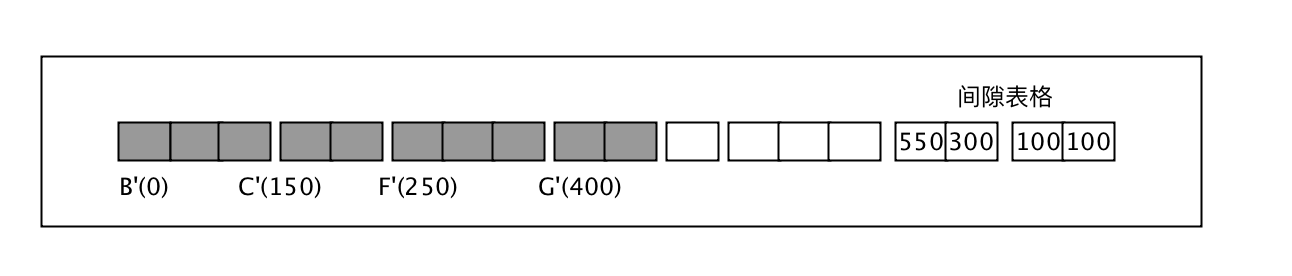
间隙表格

第二步更新指针的伪代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
adjust_ptr() {
    for(r : $roots)
        *r = new_address(*r)
    
    scan = $heap_start
    # 对活动对象更新指针
    while(scan < $free)
        scan.mark = FALSE
        for(child : children(scan))
            *child = new_address(*child)
        scan += scan.size
}

# 找到活动对象对应的应该跟新到的指针地址
new_address(obj) {
    best_entry = new_bt_entry(0,0)
    for(entry : break_table)
        if(entry.address <= obj && $best_entry.address < entry.address)
            best_entry = entry
    return obj - best_entry.size
}

上面的new_address函数比较难理解，就是需要从多个间隙表格中找到活动对象群所对应的，然后利用obj-best_entry.size 就返回节点对应的新地址。

优点: 首先内存利用率和Two-Finger一样，但是由于是保持了原来的顺序，所以可以利用缓存。
缺点: 每次移动都要进行表格的移动和更新，代价比较高。

ImmixGC 算法

暂略……

保守式GC

前面提到过GC是根据对象的指针指向去搜寻其他对象的。另一方面，GC对非指针不进行任何操作。另外可以认为调用栈、寄存器以及全局变量空间都是根。对于上面存在一个问题就是: 如何识别一个变量是否是指针? 这里所说的保守式GC就是指”不能识别指针和非指针的GC”, 而准确式GC指的就是能够正确识别指针和非指针的GC。

保守式GC

之前说的下面这些空间都是根:

  • 寄存器
  • 调用栈
  • 全局变量空间

但是事实上他们都是不明确的根(ambiguous roots)。
保守式GC对检查不明确的根时，所进行的基本项目是:

  • 是不是被正确对齐的值? (32位CPU，为4的倍数；64位CPU为8的倍数; 其他情况被视为非指针)
  • 是不是指着堆内? (分配了GC专用堆，对象就会被分配到堆里，指向对象的指针按道理肯定指向堆内，否则就是非指针)
  • 是不是指着对象的开头?(如果把对象固定大小对齐，例如”BiBOP”法，如果对象的值不是固定大小的倍数，就是非指针)

当不明确的根运行GC时，偶尔会出现非指针和堆里的对象的地址一样的情况，这时就无法识别这个值是非指针，这就是“貌似指针的非指针”(false pointer), 保守式GC这种把”貌似指针的非指针”看成”指向对象的指针”叫做”指针的错误识别”。在采用GC标记-清除算法，这种非指针会被错误的识别为活动对象，不会被回收。这样采取的是一种保守的态度，这样处理也不会出现问题。

  • 优点: 容易编写语言处理程序
  • 缺点: 识别指针和非指针需要付出成本;错误识别指针会压迫堆, 会占用堆空间;能够使用的GC算法有限，不能使用移动对象的GC算法，否则就会重新非指针，照成意想不到的BUG

准确式GC

准确式GC是基于正确识别指针和非指针的“正确的根”(exact roots)来执行GC的。要想创建正确的根，就需要”语言处理程序的支援”, 依赖语言处理程序的实现。常见的方法这里介绍两种：

  • 打标签: 通过打标签的方法把不明确的根里的所有非指针和指针都区别开来。

  • 不把寄存器和栈当做根: 创建一个正确的根来管理，这个正确的根在处理程序里只集合了mutator可能到达的指针，然后以它为基础执行GC。 参考Rubinius语言处理程序的实现。

  • 优点: 相对于保守式GC，能够正确识别指针和非指针，适用的GC方法也更广泛。

  • 缺点: 需要语言处理程序的支援，给实现者带来负担。

间接引用

保守式GC有一个缺点就是”不能使用GC复制算法等移动对象的算法”, 因为如果是非指针的对象发生移动，其值就会发生变化，使用这个对象就会出现问题。解决这个问题的方法就是使用”间接引用”
结合下图来说明:
复制前可以看到根和对象之间有句柄。每个对象都有一个句柄，它们分别持有指向这些对象的指针。并且局部变量和全局变量这些不明确的根里没有指向对象的指针，只装着指向句柄的指针(如图中的1，2，3), 下图中的1，2表示指针，3表示非指针。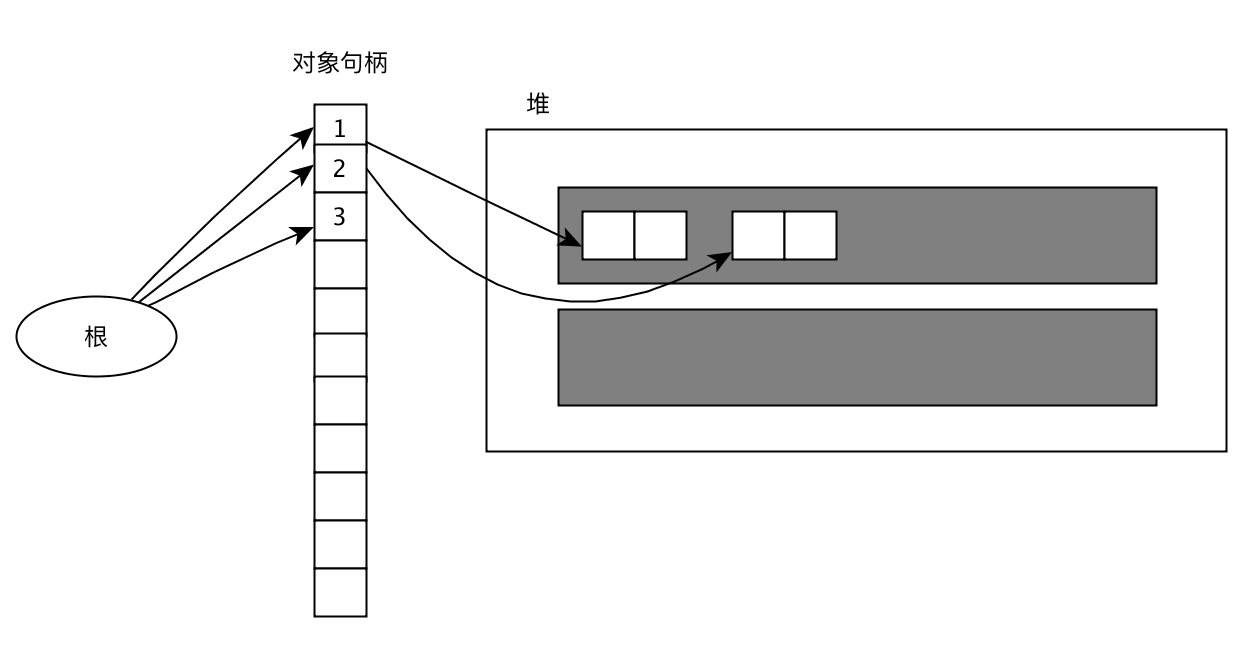
间接引用1
复制之后移动了引用目标的对象，只修改了1，2是指针的值，非指针3的值并没有发生改变。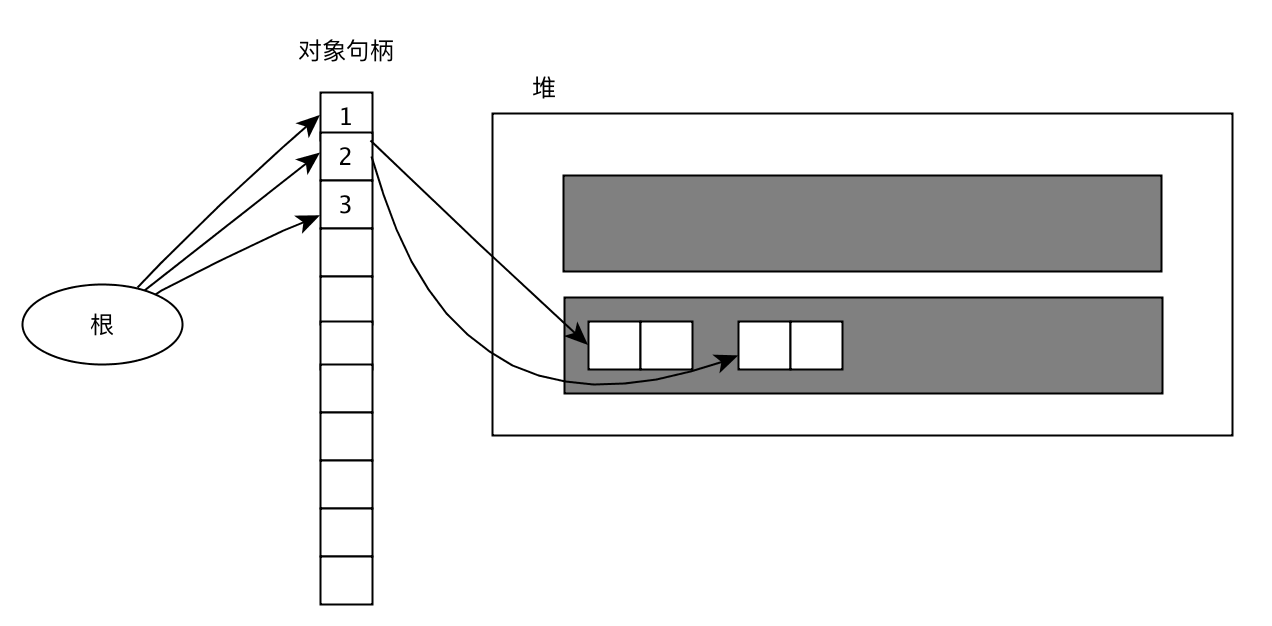
间接引用2

  • 优点: 可以适用于更多的GC算法
  • 缺点: 所有对象都要经由句柄间接引用，回拉低访问对象内数据的速度。

MostlyCopyingGC

又是一个为了能够执行GC复制算法的保守式GC, 这个算法的核心思想就是抛开那些不能移动的对象，将其他”大部分”的对象都进行复制的GC算法，目的是为了保证不能移动的对象一定不会移动，可以移动的对象大部分都移动了，保证不出现BUG。
这个算法执行的前提条件:

  1. 根是不明确的根
  2. 没有不明确的数据结构
  3. 对象大小随意

执行这个算法的要点是把堆分配成一定大小的页(page)组成，执行分配的时候从正在使用的页里分配，如果空间不够则使用空页，如果一个页放不下，则会跨页存储。
执行GC时把所有根直接引用的页升级为To空间，然后再把To页对象的子对象复制到空页。这个过程会保留根直接引用的对象，所以不会复制非指针对象。同时升级的页中也包含了垃圾对象吗，无法清除。

黑名单

保守式GC指针的错误识别所带来害处和这个对象的大小及其子对象的数量有关系，如果一个对象很大，或者子对象很多，却被识别为”还活着”, 那就会在占用很多的堆空间。
这里的黑名单记录的是”不明确的根内的非指针，其指向的是有可能被分配对象的地址”， 这里说的”有可能被分配对象的地址”指的是”堆内未使用的对象的地址”。mutator无法引用至今未使用过的对象。也就是说，如果根里存在有这种地址的指针，那它肯定就是”非指针”，就会被记入黑名单中。在分配对象过程中，如果要分配的地址在黑名单中，这个对象有可能被非指针值所引用。也就是说，及时分配后对象成了垃圾，也很有可能被错误识别为”还活着”。为此，对象分配到这种地址是要满足:

  • 小对象
  • 没有子对象的对象

这样及时错误识别了，对整个堆的影响也不大，把对堆的压迫控制在最低限度。

分代垃圾回收

分代垃圾回收(Generational GC)把对象按“年龄”进行分类，使用不同的GC算法, 提高垃圾回收的效率。年龄的概念就是指对象的生存时间，经历一次GC后活下来的对象年龄就是1，依次类推。 新生成的对象和年龄小于一定值得对象都称为新生代对象, 年龄大于一定值得对象则称为老年代对象, 这就是所谓的分代。新生代对象经历一定GC后会变成老年代对象，这个过程就叫晋升(promotion)。

Ungar 的分代垃圾回收

Ungar 的垃圾回收是针对新生代执行GC复制算法，针对老年代执行标记-清除算法。Ungar 将堆结构分为四个部分，分别是生成空间、2个大小相等的幸存空间以及老年代空间，并分别用$new_start、$survivor1_start、$survivor2_start、$old_start这4个变量引用它们的开头。将生成空间和幸存空间合称为新生代空间。
当生成空间满了的时候，新生代GC就会启动，将生成空间的所有活动对象复制，这根GC复制算法是一个道理。目标空间是幸存空间中空闲的一个。

      记 录 集
    +---+---+---+---+
$rs |   |   |   |   |
    +---------------+
    +------------------------+ $new_start
    |              +--------------+   $survivor1_start
    |              |     +-------------+ $survivor2_start
    |              |     |     +-----------+  $old_start
    |              |     |     |                           堆
    v--------------v-----v-----v-----------------------------+
    |              |     |     |                             |
    |              |     |     |                             |
    |              |     |     |                             |
    +--------------+-----+-----+-----------------------------+
     生 成 空 间     幸 存 空 间            老 年 代 空 间
           新 生 代 空 间

分代垃圾回收的优点是只将垃圾回收的重点放在新生代对象上，以此来缩减GC所需的时间。但是老年代有可能引用了新生代对象，所以还需要遍历老年代对象，这样就大大削减了分代垃圾回收的优势，所以为了解决这个问题，又增加了一个记录集。记录集里记录的是对新生代有引用的老年代对象。这样在新生代GC时，只需要再对记录集进行遍历就行了。
为了将老年代对象记录到记录集里，我们利用写入屏障(write barrier)。在mutator更新对象间的指针操作中，写入屏障是不可或缺的。

1
2
3
4
5
6
7
8
9
write_barrier(obj, field, new_obj) {
    if(obj >= $old_start #发出引用的对象在老年代里
        && new_obj < $old_start #新生成的对象在新生代里
        && obj.remembered == FALSE) #老年代对象没有被记录
        $rs[$rs_index] = obj #老年代对象加入记录集
        $rs_index++ 
        obj.remembered = TRUE #表示已经被记录过
    *field = new_obj #field是obj的指针，更新指针new_obj成为引用目标的对象
}

分配是在生成空间进行的，执行分配的new_obj()函数伪代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
new_obj(size) {
    if($new_free + size >= $survivor1_start)
        # 生成空间不够用，执行新生代GC
        minor_gc()
        if($new_free + size >= $survivor1_start)
            # 执行GC后仍然不够用，返回错误
            allocation_fail()
    
    obj = $new_free #$new_free 是指向生成空间的分块开头的指针
    $new_free += size
    obj.age = 0 #年龄默认值
    obj.forwarded = FALSE #防止重复复制相同对象的标志，跟GC复制算法和GC标记-压缩算法中的作用一样
    obj.remembered = FALSE #是否在记录集里，只用于老年代对象
    obj.size = size
    return obj
}

新生代GC的伪代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
minor_gc() {
    $to_survivor_free = $to_survivor_start
    #根在新生代的对象进行GC复制
    for(r : $roots)
        if(*r < $old_start)
            *r = copy(*r)

    i = 0
    #对记录集里的对象的子节点进行GC复制
    while(i < $rs_index)
        has_new_obj = FALSE
        for(child : children($rs[i]))
            if(*child < $old_start)
                *child = copy(*child)
                if(*child < $old_start)
                    has_new_obj = TRUE
        # TRUE表示复制后的对象在新生代，FALSE表示复制后的对象在老年代
        # 复制后的对象在老年代，则需要把这个对象从记录集里去掉
        if(has_new_obj == FALSE)
            $rs[i].remembered = FALSE
            $rs_index--
            #最后一位与当前节点交换，交换后，最后一位无法在访问到，可以认为是从记录集里去掉了
            swap($rs[i], $rs[$rs_index])
        else
            i++
    #交换From空间和To空间
    swap($from_survivor_start, $to_survivor_start)
}

# 对象的复制
copy(obj) {
    #没有被复制
    if(obj.forwarded == FALSE)
        #年龄没有达到
        if(obj.age < AGE_MAX)
            copy_data($to_survivor_free, obj, obj.size)
            # 标识已经被复制
            obj.forwarded = TRUE
            # 被复制到的地址
            obj.forwarding = $to_survivor_free
            # age++
            $to_survivor_free.age++
            $to_survivor_free += obj.size
            for(child : children(obj))
                *child = copy(*child)
        else
            # 年龄达到，晋升到老年代
            promote(obj)
    return obj.forwarding
}

# 对象从新生代晋升到老年代
promote(obj) {
    #从老年代找空间
    new_obj = allocate_in_old(obj)
    if(new_obj == NULL)
        #空间不够执行老年代的GC，跟GC标记-清除法一样
        major_gc()
        new_obj = allocate_in_old(obj)
        if(new_obj == NULL)
            allocation_fail()
    obj.forwarding = new_obj
    obj.forwarded = TRUE

    for(child : children(new_obj))
        if(*child < $old_start)
            $rs[$rs_index] = new_obj
            $rs_index++
            new_obj.remembered = TRUE
            return
}

分代垃圾回收是建立在”很多对象年纪轻轻就会死”的基础上的，所以满足这种条件时，可以改善GC所花费的时间，提高吞吐量。是但是因为老年代GC很费时，所以没办法缩短mutator的最大暂停时间。并且如果不满足上面的条件时，就没办法利用到分代垃圾回收的优势。

记录各代之间的引用的方法

Ungar 分代垃圾回收的记录集是不可少的，但是这个记录集会浪费很多空间，为了提高内存利用率，可以通过下面两种方法：

  • 卡片标记: 把老年代空间等分成N个卡片，每份假设129字节(1024位)，可以用表格表格中位图的一位表示一个卡片，这样能够有效提高内存空间(只需老年代的1/1024)。当标记表格设置很多位时，可能就会在搜索卡片上花费大量时间。
  • 页面标记: 利用OS的页面管理，如果在卡片标记中奖卡片和页面设置为同样大小，我们就能得到OS的帮助。一旦mutator对堆内的某一个页面进行写入操作，OS就会设置跟这个页面对应的位，我们把这个位叫做页面重写标志位(dirty bit)。卡片标记中是搜索标记表格，而页面标记则是搜索这个页面的重写标志位。

多代垃圾回收

分代垃圾回收是把对象分为新生代和老年代两个，也可以分成3个及更多个, 分代越多，对象变成垃圾的机会也就越大，所以这个方法确实能够减少活到最老代的对象。但是每代的空间也就相应的变小了，这样一来各代之间的引用就变多了，各代中垃圾回收花费的时间也就越来越长了。综合来看，少设置一些分代能得到更优秀的吞吐量，据说分为2代或3代是最好的。

列车垃圾回收

Ungar 分代垃圾回收的一个问题是不能够减少最大暂停时间，而列车垃圾回收(Train GC)就是为了控制老年代GC中暂停时间的增长而设计的。列车垃圾回收中将老年代空间按照一定的大小划分，每个划分出来的空间称为车厢，多个车厢有组成列车，多个列车一起组成了老年代空间。1次老年代GC不再是对整个老年代空间进行，而是以1个车厢作为GC对象。
下面这幅图反应的是列车垃圾回收的堆结构: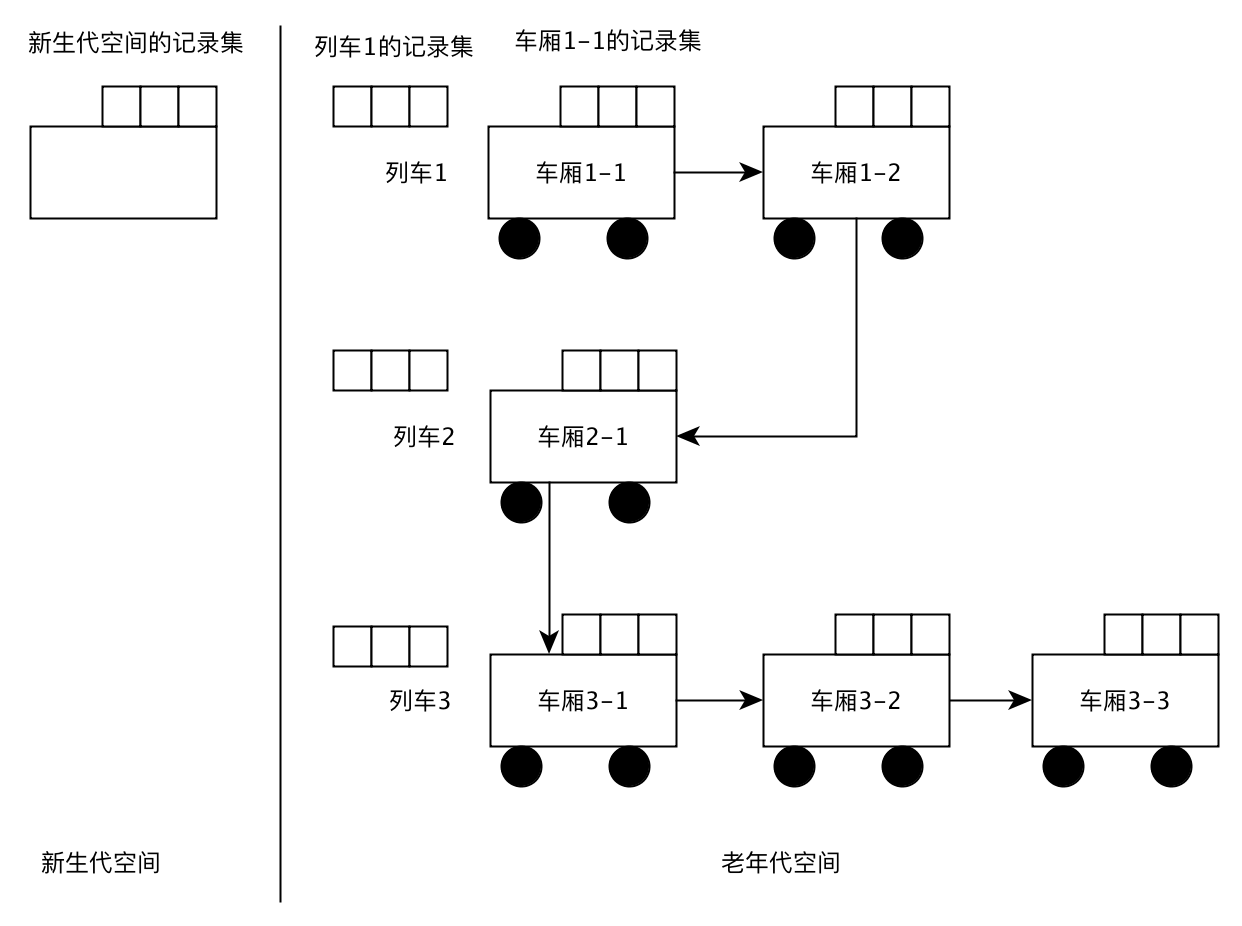
列车垃圾回收堆结构
具体过程省略……

  • 优点: 缩减了老年代GC照成的mutator的最大暂停时间。还能回收循环的大型垃圾。
  • 缺点: 执行写入屏障的额外负担要比Ungar的分代垃圾回收中执行时所产生的更大，因此吞吐量上要弱一些。

增量式垃圾回收

增量式垃圾回收(Incremental GC)是一种通过逐渐推进垃圾回收来控制mutator最大暂停时间的方法。之前介绍的GC算法，一旦GC开始执行，mutator就没有办法执行了，像这样的GC叫做听执行GC。为了改变这种方式，想出了一种GC和mutator交替运行的方式，这就是增量垃圾回收。

三色标记算法

这个算法将GC中的对象按照各自情况分成三种:

  • 白色: 还未搜索过的对象
  • 灰色: 正在搜索的对象
  • 黑色: 搜索完成的对象

以GC标记-清除算为例，应用到三色标记算法中。默认对象都是白色，GC一旦运行，所有从根能够到达的对象都会被标记，然后放到栈里。放到栈里的对象被标记成灰色，然后栈里的对象依次弹出，搜索其子对象，子对象也被标记成灰色。当其所有的子对象都被标记成灰色时，该对象就被标记成黑色。当GC结束时已经不存在灰色对象了，活动对象全部为黑色，垃圾对象则为白色。
增量式的GC标记-清除算法可以分为以下三个阶段:

  • 根查找阶段
  • 标记阶段
  • 清除阶段

下面是过程的伪代码，所谓标记为灰色并不是真正的标记为灰色，而是标记位TRUE,并放到栈中；置为黑色则只是标记为TRUE; 标记位白色的就是obj.mark=FALSE

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
incremental_gc() {
    case $gc_phase
    when GC_ROOT_SCAN
        root_scan_phase() #根查找阶段
    when GC_MARK
        incremental_mark_phase() #增量标记阶段
    else
        incremental_sweep_phase() #增量清除阶段
}

#根查找函数
root_scan_phase() {
    for(r : $roots)
        mark(*r)
    $gc_phase = GC_MARK
}

mark(obj) {
    if(obj.mark == FALSE)
        obj.mark = TRUE
        push(obj, $mark_stack) #灰色对象放到栈里
}

#增量标记
incremental_mark_phase() {
    for(i : 1..MARK_MAX) # MARK_MAX每次从栈中弹出对象的次数
        if(is_empty($mark_stack) == FALSE)
            obj = pop($mark_stack) #从栈中弹出灰色对象, 标记其子对象
            for(child : children(obj))
                mark(*child)
        else
            #栈为空，重新从根开始查找
            for(r : $roots)
                mark(*r)
            #从根查找完继续标记
            while(is_empty($mark_stack) == FALSE)
                obj = pop($mark_stack)
                for(child : children(obj))
                    mark(*child)
        #为清除阶段做准备
        $gc_phase = GC_SWEEP
        $sweeping = $heap_start
        return
}

#写入屏障，对于新节点，需要标记为灰色
#如果没有这一步，标记阶段进行到一半有可能不会对新的节点进行搜索
write_barrier(obj, field, newobj) {
    if(newobj.mark == FALSE)
        newobj.mark = TRUE
        push(newobj, $mark_stack)

    *field = newobj
}

#清除阶段
incremental_sweep_phase() {
    swept_count = 0
    while(swept_count < SWEEP_MAX) #每次清除SWEEP_MAX个对象
        if($sweeping < $heap_end)
            if($sweeping.mark == TRUE)
                $sweeping.mark = FALSE
            else
                #mark=false表示白色，放入到空闲链表中
                $sweeping.next = $free_list
                $free_list = $sweeping
                $free_size += $sweeping.size

            $sweeping += $sweeping.size
            swept_count++
        else
            $gc_phase = GC_ROOT_SCAN
            return

}

#分配
newobj(size) {
    #$free_siz 小于一定量时就执行GC， 而不是等到空间枯竭
    if($free_size < HEAP_SIZE * GC_THRESHOLD)
        incremental_gc()
    
    chunk = pickup_chunk(size, $free_list)
    if(chunk != NULL)
        chunk.size = size
        $free_size -= size
        #chunk如果在清除阶段在要清除的空间，需要涂黑，表示不可回收
        if($gc_phrase == GC_SWEEP && $sweeping <= chunk)
            chunk.mark = TRUE
            return chunk
        else
            allocation_fail()
}

可以看到上面整个过程，分配和GC是交替进行的，而且GC的三个阶段也是按顺序循环进行的，每次执行incremental_gc()都会进入下一个阶段。

  • 优点: 增量式垃圾回收不是一口气运行GC,而是和mutator交替运行的，因此不会长时间妨碍到mutator的运行。
  • 缺点: 牺牲了吞吐量。吞吐量和最大暂停时间是互相权衡的，一方面做的好另一方面就会变差。

Steele的算法

这个算法中使用的写入屏障要比上面(Dijkstra)的写入屏障条件更严格，它能减少GC中错误的标记的对象。
这个算法的标记函数如下:

1
2
3
4
mark(obj) {
    if(obj.mark == FALSE)
        push(obj, $mark_stack)
}

可以看出在放入栈时并没有标记obj.mark=TRUE, 也就是说这个算法的灰色对象是指”堆在标记栈里的没有设置标志位的对象”, 黑色对象是”设置了标志位的对象”。
写入屏障的伪代码也不一样:

1
2
3
4
5
6
7
8
9
write_barrier(obj, field, newobj) {
    if($gc_phase == GC_MARK &&
        obj.mark == TRUE &&
        newobj.mark == FALSE)
        obj.makr = FALSE
        push(obj, $mark_stack)

    *field = newobj
}

上面代码主要是判断如果在标记过程中发出引用的对象是黑色对象，且新的引用的目标对象为灰色或白色，那么我们就把发出引用的对象涂成灰色。Steele的写入屏障通过限制标记对象来减少被标记的对象，从而防止了因疏忽而造成垃圾残留的后果。 (详情参见P175)

汤浅的算法

汤浅的算法中标记阶段并没有在搜索根，遵循了”以GC开始时对象间的引用关系为基础执行GC”这项原则。

1
2
3
4
5
6
7
8
9
10
11
incremental_mark_phase() {
    for(i : 1..MARK_MAX)
        if(is_empty($mark_stack) == FALSE)
            obj = pop($mark_stack)
            for(child : children(obj))
                mark(*child)
    else
        $gc_phrase = GC_SWEEP
        $sweeping = $heap_start
        return
}

上面通过写入屏障防止产生从黑色对象指向白色对象的指针，而汤浅的算法中却允许黑色对象指向白色对象的指针。汤浅算法是基于在GC开始时保留活动对象这项原则，就没有必要在生成新指针时标记引用对象的目标了。及时出现了从黑色对象指向白色对象的指针，只要保留了GC开始时的指针，作为引用目标的白色对象早晚会被标记。但是在删除指针时无法保留指针，因此写入屏障要进行一些特殊处理:

1
2
3
4
5
6
7
8
9
write_barrier(obj, field, newobj) {
    oldobj = *field
    #在标记阶段中如果指针更新前引用的oldobj是白色对象，就将其涂成灰色
    if(gc_phase == GC_MARK && oldobj.mark == FALSE)
        oldobj.mark = TRUE
        push(oldobj, $mark_stack)

    *field = newobj
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#分配
newobj(size) {
    if($free_size < HEAP_SIZE  * GC_THRESHOLD)
        incremental_gc()

    chunk = pickup_chunk(size, $free_list)
    if(chunk != NULL)
        chunk.size = size
        $free_size -= size
        #这里跟之前不一样，分配后会设置obj为黑色
        if($gc_phase == GC_MARK)
            chunk.mark = TRUE
        else if($gc_phase == GC_SWEEP && $sweeping <= chunk)
            chunk.mark = TRUE
        return chunk
    
    else
        allocation_fail()
}

RC Immix算法

gc